某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境:
如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M处,连接BF与EG交于点P.
所得结论:
当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):
甲:△AEF的边AE= cm,EF= cm;
乙:△FDM的周长为16 cm;
丙:EG=BF.
你的任务:填充甲同学所得结果中的数据;
写出在乙同学所得结果的求解过程;
当点F在AD边上除点A、D外的任何一处(如图2)时:
① 试问乙同学的结果是否发生变化?请证明你的结论;
② 丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?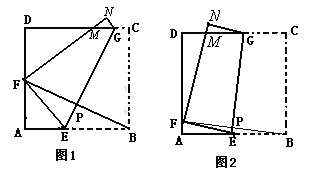
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;(2)以图中的点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.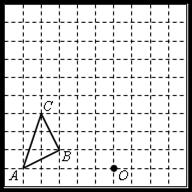
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)画出图形。
写出B、C两点的对应点B'、C'的坐标;如果△OBC内部一
 点M的坐标为(x,y),写出M的对应点M'的坐标。
点M的坐标为(x,y),写出M的对应点M'的坐标。
(本题满分12分, 第(1)小题4分,第(2)小题4分,第(3)小题4分)
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
如图,在△ABC中,∠C=90°,D、E分别为AB、AC边上的两点,且AD·AB=AE·AC,求证:DE⊥AB.
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),(正方形网格中,每个小正方形的边长是1个单位长度)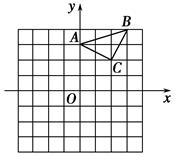
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2∶1,并直接写出C2点的坐标及△A2BC2的面积.
已知格点△ABC.
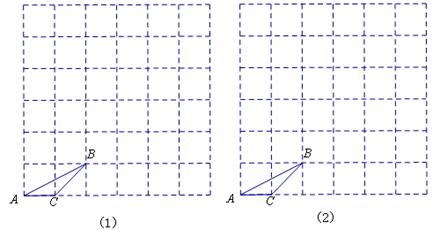
(1)画出与△ABC相似的格点△A1B1C1,使△A1B1C1与△ABC的相似比为2;
(2)画出与△ABC相似的格点△A2B2C2,使△A2B2C2与△ABC的相似比为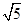 ;
;
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
当AD=3时,求DE的长;
当点
 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设 ,
, ,
,
求 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
在点E、F移动过
 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.

如图,A、D、F、B在同一直线上,AE=BC,且AE∥BC,AD=BF.
(1)求证: ;
;
(2)连ED,CF,则四边形EDCF是 .(从平行四边形,矩形,菱形,正方形中选填).
在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N .写出点C的坐标;
求证:MD = MN;
连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明.

已知△ABC,∠ACB=90º,AC=BC,点E、F在AB上,∠ECF=45º,设△ABC的面积为S,说明AF·BE=2S的理由。