上海市闸北九年级期末考试数学试卷
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG︰AD是( )
| A.2︰3 ; | B.1︰2; | C.1︰3 ; | D.3︰4. |
已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
(A)BD︰AB = CE︰AC; (B)DE︰BC = AB︰AD;
(C)AB︰AC = AD︰AE; (D)AD︰DB = AE︰EC.
下列有关向量的等式中,不一定成立的是( )
A. =- =- ; ; |
B.︱ ︱=︱ ︱=︱ ︱; ︱; |
C. + + = = ; ; |
D.︱ + + ︱=︱ ︱=︱ ︱+︱ ︱+︱ |. |. |
在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是( )
(A)cosA=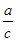 ; (B)tanA=
; (B)tanA= ; (C)sinA=
; (C)sinA=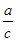 ; (D)cotA=
; (D)cotA=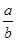 .
.
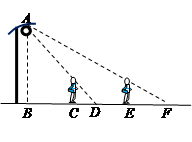
如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米.他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米.已知小明的身高是1.5米,那么路灯A的高度AB是( )
| A.4.5米; | B.6米; | C.7.2米; | D.8米. |
如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,若
S△AFD=9,则S△EFC= .
已知抛物线经过A(0,-3)、B(2,-3)、C(4,5),判断点D(-2,5)是否在该抛物线上.你的结论是: (填“是”或“否”).
如图,梯形ABCD中,AD//BC,AB=DC,点P是AD边上一点,联结PB、PC ,且 ,则图中有 对相似三角形.
,则图中有 对相似三角形. 
如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果 ,
, .那么m与n满足的关系式是:m= (用含n的代数式表示m).
.那么m与n满足的关系式是:m= (用含n的代数式表示m).
(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设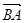 =
=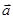 ,
,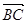 =
=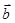 ,试用
,试用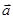 、
、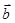 分别表示向量
分别表示向量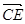 和
和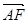 .
. 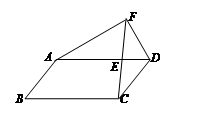
如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
(本题满分12分, 第(1)小题4分,第(2)小题4分,第(3)小题4分)
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
(本题满分12分, 第(1)小题6分,第(2)小题6分)
如图,在平面直角坐标系内,已知直线 与x轴、y轴分别相交于点A和点C,抛物线
与x轴、y轴分别相交于点A和点C,抛物线 图像过点A和点C,抛物线与x轴的另一交点是B,
图像过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
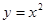 ;
;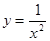 ;
;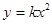 ;
;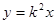 .
. =
= ,则
,则 的值是 .
的值是 . 的比值是 .
的比值是 .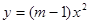 的开口向上,那么m的取值范围是 .
的开口向上,那么m的取值范围是 .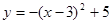 向下平移6个单位,所得到的抛物线的顶点坐标为 .
向下平移6个单位,所得到的抛物线的顶点坐标为 .
 -
- =2.
=2.

 =
= 时,求x的值
时,求x的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号