(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数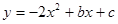 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
相关知识点
推荐套卷
(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数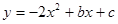 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.