[山东]2011—2012学年山东省威海八年级下数学期末模拟试卷(二)
用两个全等的等边三角形,可以拼成下列哪种图形( )
| A.矩形 | B.菱形 | C.正方形 | D.等腰梯形 |
小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )
| A.众数 | B.平均数 | C.加权平均数 | D.中位数 |
王英在荷塘边观看荷花,突然想测试池塘的水深,她把一株竖直的荷花(如右图)拉到岸边,花柄正好与水面成600夹角,测得AB长60cm,则荷花处水深OA为( )
| A.120cm | B. cm cm |
C.60cm | D.cm |

如图,□ABCD的对角线AC、BD相交于O,EF过点O与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A、16 B、14 C、12 D、10
已知a= ,b=
,b= ,用含a、b的代数式表示
,用含a、b的代数式表示 ,这个代数式是( )
,这个代数式是( )
| A.a+b | B.ab | C.2a | D.2b |
如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,若∠B=700,则∠EDC的大小为
| A.100 | B.150 | C.200 | D.300 |

若x2+mx+3=(x+3)(x+1),则方程mx2+3mx+8=0的两个根是( ).
| A.x1=1,x2=2 | B.x1=-1,x2=-2; | C.x1=1,x2=-2 | D.x1=-1,x2=2 |
下列命题正确的是
| A.同一边上两个角相等的梯形是等腰梯形; |
| B.一组对边平行,一组对边相等的四边形是平行四边形; |
| C.如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形。 |
| D.对角线互相垂直的四边形面积等于对角线乘积的一半。 |
甲、乙两班举行班际电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表: 
通过计算可知两组数据的方差分别为 ,
, ,则下列说法:①两组数据的平均数相同;②甲组学生比乙组学生的成绩稳定;③两组学生成绩的中位数相同;④两组学生成绩的众数相同。其中正确的有
,则下列说法:①两组数据的平均数相同;②甲组学生比乙组学生的成绩稳定;③两组学生成绩的中位数相同;④两组学生成绩的众数相同。其中正确的有
| A.1个 | B.2个 | C.3个 | D.4个 |
将4个数 排成2行、2列,两边各加一条竖直线记成
排成2行、2列,两边各加一条竖直线记成 ,定义
,定义
 ,上述记号就叫做2阶行列式.若
,上述记号就叫做2阶行列式.若
 ,则
,则 .
.
下面是马虎同学在一次测验中解答的填空题:
①若x2=a2,则x=a;②方程2x(x-1)=x-1的解为x=1;③若x4-2x2-3=0,令 则a=3或-1.④经计算整式
则a=3或-1.④经计算整式 与
与 的积为
的积为 .则一元二次方程
.则一元二次方程 的所有根是
的所有根是 ,
, 。则其中答案完全正确的题目为_______(将正确结论的序号填写在横线上)
。则其中答案完全正确的题目为_______(将正确结论的序号填写在横线上)
红丝带是关注艾滋病防治问题的国际性标志.将宽为1cm的红丝带交叉成60°角重叠在一起(如图),则重叠四边形的面积为 cm2.
在课外活动课上,老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm2,则对角线所用的竹条至少需 cm
在解方程x2+px+q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,解得方程的根为4与-2。这个方程的根应该是什么?
如图,网格中每一个小正方形的边长为1个单位长度.AB的长度为 .
请在所给的网格内画出以线段AB为腰、BC为下底的
等腰梯形ABCD;梯形ABCD的面积等于_________.

如图,将一张矩形纸片 沿EF折叠,使点
沿EF折叠,使点 落在
落在 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点 落在点D处,且BD过F点.
落在点D处,且BD过F点.
试判断四边形BEFG的形状,并证明你的结论.
当∠BFE为多少度时,四边形BEFG是菱形.

四川汶川大地震牵动了三百多万滨州人民的心,全市广大中学生纷纷伸出了援助之手,为抗震救灾踊跃捐款。滨州市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据。下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人。他们一共调查了多少人?
这组数据的众数、中位数各是多少?
若该校共有1560名学生,估计全校学生捐款多少元?

阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
 的有理化因式是 .
的有理化因式是 .  分母有理化得 .
分母有理化得 .
分母有理化:(1)
 ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)"  =______..
=______..
计算:
 .
.
已知关于x的一元二次方程x2+4x+m-1=0。请你为m选取一个合适的整数,使得到的方程有两个不相等的实数根;
设α、β是(1)中你所得到的方程的两个实数根,求α2+β2+αβ的值。
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律:
根据以上规律,回答以下问题:商高数的三个数中,有几个偶数,几个奇数?
写出各数都大于30的两组商高数。
用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
已知:在四边形ABCD中,AC = BD,AC与BD交于点O,∠DOC = 60°.当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.



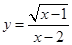 的自变量
的自变量 的取值范围是____________.
的取值范围是____________. +
+ =________.
=________.
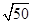 ,宽b=3
,宽b=3 ,则面积S=________.
,则面积S=________. (用配方法解)
(用配方法解) (用公式法解)
(用公式法解)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号