江苏省扬州市宝应县九年级上学期期末测试数学试卷
一元二次方程x2-8x+5=0的左边配成完全平方后所得的方程是( )
| A.(x-6)2=11 | B.(x-4)2=11 |
| C.(x-4)2=21 | D.以上答案都不对 |
有下列四个命题:
①直径是弦;
②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;
④半径相等的两个半圆是等弧.
其中正确的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
关于x的一元二次方程(m-2)x2+x+m2-4=0的一个根是0,则m的值为( )
| A.2或-2 | B. |
C.-2 | D.2. |
10名九年级学生的体重分别是41,48,50,53,49,50,53,67,51,53(单位:kg).这组数据的极差是( )
| A.26 | B.25 | C.24 | D.12 |
如图,已知AB为⊙O的直径,点C、D在⊙O上,∠ABC=50°,则∠D的度数为( )
A.30° B.40° C.50° D.60°
如图是二次函数y=ax2+bx+c的图象,下列关系中,正确的是( )
| A.a>0且c<0 | B.a<0且c<0 |
| C.a<0且c>0 | D.a>0且c>0 |
如图,⊙O过正方形ABCD的顶点A、B,且与CD相切,若正方形ABCD的边长为2,则⊙O的半径为( )
A.1 B. C.
C. D.
D.
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A. |
B. |
C. |
D. |
跳远运动员李刚对训练效果进行测试,6次跳远的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9.(单位:m)这六次成绩的平均数为7.8,方差为 ,.如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差 (填“变大”、“不变”或“变小”).
如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,点E、F分别是BO、BC的中点,若AB=6cm,则△BEF的周长为 
如图,Rt△AOB中,∠O=90°,OA=OB=3 ,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为 
要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是 m.
,那么截成的两段铜丝的长度差应是 m.
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
10 |
5 |
2 |
1 |
2 |
5 |
… |
若A(m,y1),B(m+1,y2)两点都在该函数的图象上,当m= 时,y1=y2.
如图,以半圆的一条弦BC为对称轴将弧BC折叠后与直径AB交于点D,若AD=4,BD=8,则CB的长为 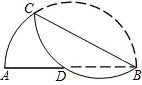
已知关于x的方程x2+ax+a-2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.
(1)求证:四边形AECD是矩形;
(2)当△ABC满足什么条件时,矩形AECD是正方形,并说明理由.
有A、B两个黑布袋,A布袋中有两个除标号外完全相同的小球,小球上分别标有2、3.B布袋中也有两个除标号外完全相同的小球,小球上分别标有1、2.小明先从A布袋中随机取一个小球,用a表示取出的小球上标有的数字,再从B布袋中取出一个小球,用b表示取出的球上标有的数字.
(1)请你用画树形图法或列表法求出a与b的积为奇数的概率.
(2)关于x的一元二次方程x2-ax+b=0有实数根的概率为 (直接写出答案).
一个两位数的两个数字之和为9,把这个两位数的个位数字与十位数字互换得到一个新的两位数,他与原两位数的积为1458,求原两位数.
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
(1)利用网格图确定该圆弧所在圆心D点的位置(保留画图痕迹),则写出D点坐标为 ;
(2)连结AD,CD,求⊙D的半径长为 (结果保留根号),∠ADC的度数为 ;
(3)求扇形DAC是一个圆锥的侧面展开图,求该圆锥的底面半径长.(结果保留根号)
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.
如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 .
.
(1)求证:DC是⊙O的切线;
(2)如果AC∥BD,证明四边形ACDB是平行四边形,并求其周长.
如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高OA为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
已知正方形OABC中,O为坐标原点,点A在y轴的正半轴上,点C在x轴的正半轴上,点B(4,4).二次函数y=- x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
(1)求此二次函数的解析式;
(2)如图①,过点P作AP的垂线与线段BC交于点G,当点P在线段OC(点P不与点C、O重合)上运动至何处时,线段GC的长有最大值,求出这个最大值;
(3)如图②,过点O作AP的垂线与直线BC交于点D,二次函数y=- x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号