如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 .
.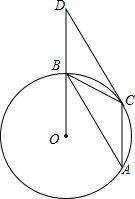
(1)求证:DC是⊙O的切线;
(2)如果AC∥BD,证明四边形ACDB是平行四边形,并求其周长.
相关知识点
推荐套卷
如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 .
.
(1)求证:DC是⊙O的切线;
(2)如果AC∥BD,证明四边形ACDB是平行四边形,并求其周长.