如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作: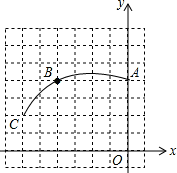
(1)利用网格图确定该圆弧所在圆心D点的位置(保留画图痕迹),则写出D点坐标为 ;
(2)连结AD,CD,求⊙D的半径长为 (结果保留根号),∠ADC的度数为 ;
(3)求扇形DAC是一个圆锥的侧面展开图,求该圆锥的底面半径长.(结果保留根号)
相关知识点
推荐套卷
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
(1)利用网格图确定该圆弧所在圆心D点的位置(保留画图痕迹),则写出D点坐标为 ;
(2)连结AD,CD,求⊙D的半径长为 (结果保留根号),∠ADC的度数为 ;
(3)求扇形DAC是一个圆锥的侧面展开图,求该圆锥的底面半径长.(结果保留根号)