如图,在△ABC中,D、E分别是AC、AB边上的点,ÐAED=ÐC,AB=6,AD=4,
AC="5," 求AE的长.
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为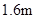 的小明
的小明 的影子
的影子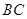 长是
长是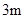 ,而小亮
,而小亮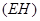 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方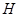 点,并测得
点,并测得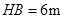 .
.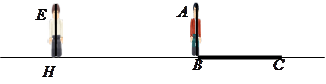
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置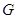 ;
;
(2)求路灯灯泡的垂直高度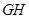 .
.
(本小题满分5分)
如图,□ABCD中,点E在BA的延长线上,连接CE,与AD相交于点F.
(1)求证:△EBC∽△CDF;
(2)若BC=8,CD=3,AE=1,求AF的长.
已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k.
(1)如果CD和C′D′是它们的对应高,那么 等于多少?
等于多少?
(2)如果CD和C′D′是它们的对应角平分线,那么 等于多少?如果CD和C′D′是它们的对应中线呢?
等于多少?如果CD和C′D′是它们的对应中线呢?
把两个含有30°角的直角三角板如图放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由. 
已知:如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED =∠B.若AE=5,AB=9,CB=6.
(1)求证:△ADE∽△ACB;(2)求ED的长.
已知:如图,四边形ABCD是平行四边形,F是AB上一点,连接DF并延长交CB的延长线于E.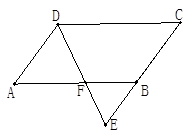
求证:AD:AF=CE:AB
如图所示,四边形ABCD∽四边形A′B′C′D′,求未知边x的长度和α的大小.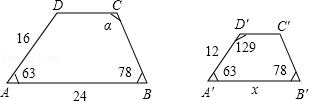
如图,在阳光下某一时刻大树AB的影子落在墙DE上的C点,同时1.2 m的标杆影长3 m,已知CD=4m,BD="6" m,求大树的高度.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证: =AB·AD;
=AB·AD;
(2)若AD=4,AB=6,求 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,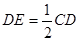 .
.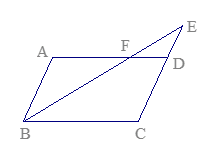
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
(满分14分)如图,已知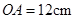 ,
,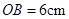 ,点
,点 从点
从点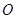 开始沿
开始沿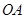 边向点
边向点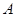 以
以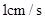 的速度移动,点
的速度移动,点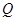 从点
从点 开始向点
开始向点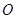 以相同的速度移动,若
以相同的速度移动,若 、
、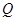 同时出发,移动时间为
同时出发,移动时间为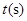 (0≤
(0≤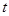 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于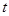 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线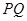 翻折后得到
翻折后得到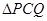 ,试判断点
,试判断点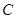 是否落在直线
是否落在直线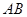 上,并说明理由.
上,并说明理由.
(3)当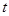 为何值时,
为何值时, 与
与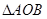 相似.
相似.
已知:ΔABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
(1)画出ΔABC向下平移4个单位得到的ΔA1B1C1。
(2)以B为位似中心,在网格中画出ΔA2BC2,使ΔA2BC2与ΔABC位似,且位似比2 :1,直接写出C2点坐标是 。
(3)ΔA2BC2的面积是 平方单位。
如图,在□ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
⑴试说明:△ABF∽△EAD;
⑵若AB=8,BE=6,AD=7,求BF的长.