[北京]2011-2012年北京海淀区九年级第一学期期末考试数学卷

下列说法正确的是 (    )

A．掷两枚硬币，一枚正面朝上，一枚反面超上是不可能事件

B．随意地翻到一本书的某页，这页的页码为奇数是随机事件

C．经过某市一装有交通信号灯的路口，遇到红灯是必然事件

D．某一抽奖活动中奖的概率为,买100张奖券一定会中奖

．下列图形中，既是轴对称图形，又是中心对称图形的是(    )

将抛物线y=x²平移得到抛物线y=x²+3,则下列平移过程正确的是 (    )

下列一元二次方程中，有两个相等的实数根的是 (    )[

已知圆锥的底面半径为2cm，母线长为5cm，则此圆锥的侧面积为(    )

如图，为了测量某棵树的高度，小明用长为2m的竹竿作测量工具，移动竹竿，使竹竿顶端、树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距6m,与树相距15m，则树的高度为(    )

已知二次函数y＝ax²＋bx＋c的图象如右图所示，则下列 结论中正确的是 (    )

A．a>0	B．c＜0
C．	D．a＋b＋c>0

已知O为圆锥顶点, OA、OB为圆锥的母线, C为OB中点, 一只小蚂蚁从点C开始沿圆锥侧面爬行到点A, 另一只小蚂蚁绕着圆锥侧面爬行到点B，它们所爬行的最短路线的痕迹如右图所示. 若沿OA剪开, 则得到的圆锥侧面展开图为 (    )

方程的解是          

如图, △ABD与△AEC都是等边三角形, 若ÐADC = 15°,则ÐABE=          ° .

若（x, y, z均不为0），则的值为           .

用两个全等的含30°角的直角三角形制作如图1所示的两种卡片, 两种卡片中扇形的半径均为1, 且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点, 按先A后B 的顺序交替摆放A、B两种卡片得到图2所示的图案. 若摆放这个图案共用两种卡片8张，则这个图案中阴影部分的面积之和为           ; 若摆放这个图案共用两种卡片(2n+1)张( n为正整数), 则这个图案中阴影部分的面积之和为         . (结果保留p )

解方程：x²-8x +1=0.

如图，在△ABC中，D、E分别是AC、AB边上的点，ÐAED=ÐC，AB=6，AD=4，
AC="5," 求AE的长．

抛物线y=ax²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

（1）根据上表填空： 
①抛物线与x轴的交点坐标是         和         ；
②抛物线经过点(-3,      )；
③在对称轴右侧，y随x增大而       ；
（2）试确定抛物线y=ax²+bx+c的解析式.

如图, 在正方形网格中，△ABC的顶点和O点都在格点上．

（1）在图1中画出与△ABC关于点O对称的△A′B′C′；
（2）在图2中以点O为位似中心，将△ABC放大为原来的2倍(只需画出一种即可).

已知关于x的方程(k-2)x²＋2(k-2)x＋k＋1=0有两个实数根，求正整数k的值

在一个口袋中有3个完全相同的小球,把它们分别标号为1, 2, 3, 随机地摸出一个
小球记下标号后放回, 再随机地摸出一个小球记下标号, 求两次摸出小球的标号
之和等于4的概率．

某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w(双)
与销售单价x(元)满足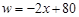(20≤x≤40),设销售这种手套每天的利润为y（元）.
（1）求y与x之间的函数关系式；
（2）当销售单价定为多少元时, 每天的利润最大？最大利润是多少？

已知二次函数y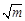＝x²+(3-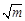)x-3(m>0)的图象与x轴交于点 (x₁, 0)和(x₂, 0),
且x₁<x₂.
（1）求x₂的值;
（2）求代数式的值.

如图，AB是⊙O的直径，点C在⊙O上，CE^AB于E, CD平分ÐECB, 交过点B的射线于D, 交AB于F, 且BC=BD.

（1）求证：BD是⊙O的切线；
（2）若AE="9," CE="12," 求BF的长.

已知△ABC的面积为a，O、D分别是边AC、BC的中点.
（1）画图：在图1中将点D绕点O旋转180°得到点E, 连接AE、CE.
填空：四边形ADCE的面积为         ；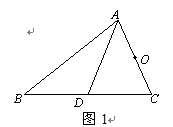

（2）在（1）的条件下，若F₁是AB的中点，F₂是AF₁的中点,F₃是AF₂的中点,…,
F_n是AF_{n -1}的中点 (n为大于1的整数), 则△F₂CE的面积为            ;
△F_nCE的面积为           .

已知二次函数y=ax²+bx+c的图象与反比例函数的图象交于点A (a, -3)，与y轴交于点B.

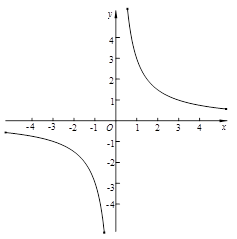
（1）试确定反比例函数的解析式;
（2）若ÐABO =135°, 试确定二次函数的解析式;
（3）在（2）的条件下,将二次函数y=ax² + bx + c的图象先沿x轴翻折, 再向右平移到与反比例函数的图象交于点P (x₀, 6) . 当x₀≤x≤3时, 求平移后的二次函数y的取值范围.

已知在□ABCD中，AE^BC于E，DF平分ÐADC 交线段AE于F.

（1）如图1，若AE=AD，ÐADC=60°, 请直接写出线段CD与AF+BE之间所满足的
等量关系;
（2）如图2, 若AE=AD，你在（1）中得到的结论是否仍然成立, 若成立,对你的结论
加以证明, 若不成立, 请说明理由；
（3）如图3, 若AE :AD =a :b，试探究线段CD、AF、BE之间所满足的等量关系，请直接写出你的结论.

如图, 已知抛物线经过坐标原点O及，其顶点为B(m,3),C是AB中点，
点E是直线OC上的一个动点 (点E与点O不重合)，点D在y轴上, 且EO=ED .

（1）求此抛物线及直线OC的解析式；
（2）当点E运动到抛物线上时, 求BD的长；
（3）连接AD, 当点E运动到何处时，△AED的面积为，请直接写出此时E点的
坐标.