[江苏]2013届江苏省泰州市姜堰区四校八年级下学期第三次联考数学试卷
下列四组线段中,不构成比例线段的一组是
| A.1 cm,2 cm,3 cm,6 cm | B.2 cm,3 cm,4 cm,6 cm |
C.1cm, cm, cm, cm, cm, cm cm |
D.1 cm,2 cm,3 cm,4 cm |
若反比例函数y= (k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是
(k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是
| A.(6,-8) | B.(-6,8) | C.(-3,4) | D.(-3,-4) |
在下列命题中,真命题是
| A.两个等腰梯形一定相似 | B.两个等腰三角形一定相似 |
| C.两个直角三角形一定相似 | D.有一个角是60°的两个菱形一定相似 |
如上右图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于点F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABC;④△ADF与△CFB.其中相似的为 
A.①④ B.①② C.②③④ D.①②③
在比例尺为1:100 000的交通图上,距离为10厘米的甲、乙两地之间的实际距离约为_______千米.
在等边△ABC中,点D、E分别在AB、AC边上,且DE∥BC.如果BC=8 cm,AD:DB=1:3,那么△ADE的周长等于_______cm.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G,已知∠CHE=120°,则∠FEG=_________________。
如图,在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则∠EBC等于______°.
如图,在已建立直角坐标系的4×4正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P、A、B为顶点的三角形与△ABC相似,则格点P的坐标是
. 
如图,在 的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
⑴以点O(0,0)为位似中心,按比例尺(OA︰OA’)1:3在位似中心的同侧将△OAB放大为△OA’B’,放大后点A、B的对应点分别为A’、B’ .画出△OA’B’,并写出点A’、B’的坐标:A’( ),B’( ).
⑵在⑴中,若 为线段
为线段 上任一点,写出变化后点
上任一点,写出变化后点 的对应点
的对应点 的坐标( ).
的坐标( ).
已知水池的容量一定,当每小时的灌水量为q=3米3时,灌满水池所需的时间为t=12小时.
⑴写出灌水量q与灌满水池所需的时间t的函数关系式;
⑵求当灌满水池所需8小时时,每小时的灌水量.
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.
如图,BD⊥AC于D点,FG⊥AC于G点,∠CBE+∠BED=180°.
⑴求证:FG∥BD;
⑵求证:∠CFG=∠BDE.
如图,在□ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
⑴试说明:△ABF∽△EAD;
⑵若AB=8,BE=6,AD=7,求BF的长.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上, 测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.
如图,一条直线与反比例函数 的图象交于A(1,4)B(4,n)两点,与
的图象交于A(1,4)B(4,n)两点,与 轴交于D点,AC⊥
轴交于D点,AC⊥ 轴,垂足为C.
轴,垂足为C.
⑴如图甲,①求反比例函数的解析式;②求n的值及D点坐标;
⑵如图乙,若点E在线段AD上运动,连结CE,作∠CEF=45°,EF交AC于F点.试说明△CDE∽△EAF;
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点(不包括射线的端点).如图1,2,3是旋转三角板得到的图形中的3种情况.
研究:
⑴三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合如图2加以证明.
⑵三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由.
⑶若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图4加以证明.
 ≤
≤ 的非负整数解的个数为
的非负整数解的个数为 



 =0有增根,则m的值是
=0有增根,则m的值是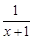 有意义,那么x的取值范围是_______.
有意义,那么x的取值范围是_______. 的图象与函数y=x的图象没有交点,那么k的取值范围是
的图象与函数y=x的图象没有交点,那么k的取值范围是  的解满足0≤x+y<2,则a的取值范围为
的解满足0≤x+y<2,则a的取值范围为  的面积为 .
的面积为 .
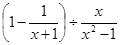 再从不等式组
再从不等式组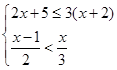 的整数解中选择一个恰当的x值代入并求值.
的整数解中选择一个恰当的x值代入并求值.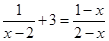
 粤公网安备 44130202000953号
粤公网安备 44130202000953号