为了测量路灯（OS）的高度,把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC）长为1米,然后拿竹竿向远离路灯方向走了3.2米（BB‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的高度.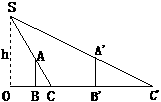
=
=
，求
的值．
，2x﹣3y+4z=22，求：代数式x+y﹣z的值．
，求
的值．相关知识点
推荐套卷
为了测量路灯（OS）的高度,把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC）长为1米,然后拿竹竿向远离路灯方向走了3.2米（BB‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的高度.
粤公网安备 44130202000953号