初中数学平行线分线段成比例解答题

已知，一次函数y=x+1的图象与反比例函数的图象都经过点A（a，2）．
（1）求a的值及反比例函数的表达式；
（2）判断点B是否在该反比例函数的图象上，请说明理由．

如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x²﹣12x+36=0的两根，BC=4，∠BAC=45°．

（1）求点A，C的坐标；
（2）反比例函数y=的图象经过点B，求k的值；
（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．

抛物线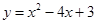与x轴交于A、B两点（点A在点B的左侧），点C是此抛物线的顶点．
（1）求点A、B、C的坐标；
（2）点C在反比例函数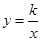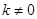（）的图象上，求反比例函数的解析式．

某食品加工厂要把600吨方便面包装后送往灾区。
（1）写出包装所需的天数t天与包装速度 y 吨/天的函数关系式；
（2）包装车间有包装工120名，每天最多包装60吨，预计最快需要几天才能包装完？
（3）包装车间连续工作7天后，为更快地帮助灾区群众，厂方决定在2天内把剩余的方便面全部包装完毕，问需要调来多少人支援才能完成任务？

在平面直角坐标系中，我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”，例如点（﹣2，﹣4），（1，2），（3，6）…都是“理想点”，显然这样的“理想点”有有无数多个．
（1）若点M（2，a）是反比例函数（k为常数，）图象上的“理想点”，求这个反比例函数的表达式；
（2）函数（m为常数，）的图象上存在“理想点”吗？若存在，请求出“理想点”的坐标；若不存在，请说明理由．

如图，一次函数y＝x＋6与反比例函数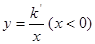的图象相交于A，B两点，与x轴、y轴交于E、F，点B的横坐标为。

（1）试确定反比例函数的解析式；
（2）求点E、F的坐标。

在复习《反比例函数》一课时，同桌的小明和小芳有一个问题观点不一致．小明认为如果两次分别从1～6六个整数中任取一个数，第一个数作为点P（m，n）的横坐标，第二个数作为点P（m，n）的纵坐标，则点P（m，n）在反比例函数y=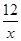的图象上的概率一定大于在反比例函数y=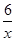的图象上的概率，而小芳却认为两者的概率相同．你赞成谁的观点？
（1）试用列表或画树状图的方法列举出所有点P（m，n）的情形；
（2）分别求出点P（m，n）在两个反比例函数的图象上的概率，并说明谁的观点正确．

如图，在平面直角坐标系xOy中，直线y=﹣x+b与x轴交于点A，与双曲线y=﹣在第二象限内交于点B（﹣3，a）．

（1）求a和b的值；
（2）过点B作直线l平行x轴交y轴于点C，求△ABC的面积．

如图，在平面直角坐标系中，一次函数y=2x+b的图象与反比例函数y=（k≠0）的图象交于A、B两点，与x轴交于点C（-2，0），点A的坐标为（n，6）．

（1）求该反比例函数的解析式；
（2）求点B的坐标，写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若点E为x轴上使△ACE为直角三角形的一点，求点E的坐标．

已知：如图，双曲线的图象经过A（1，2）、B（2，b）两点．

（1）求双曲线的解析式；
（2）当1<x<2时，反比例函数函数值的取值范围．

小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y₁=x+1的图象”的基本步骤，在纸上逐步探索函数y₂=的图象，并且在黑板上写出4个点的坐标：A（，），B（1，2），C（1，），D（﹣2，﹣1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y₁=x+1又在双曲线y₂=上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y₂=上的概率．

如果函数的图象是双曲线，且在第二、四象限内，求k的值.

如图，直线与双曲线相交于A（2，1）、B两点．

（1）求m及k的值；
（2）不解关于x、y的方程组直接写出点B的坐标；
（3）直线经过点B吗？请说明理由．

已知y与x+2成反比例，且当x=5时，y=-6，
求：（1）y与x的关系式；（2）当y=2时x的值。

已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，－3），B（4，0）．

（1）求点D的坐标；
（2）求经过点C的反比例函数解析式．