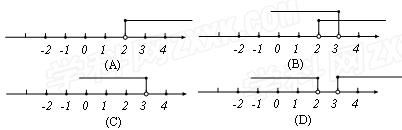
如图,直线y=x+2与双曲线y=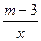 在第二象限有两个交点,那么m的取值范围在数轴上表示为(■).
在第二象限有两个交点,那么m的取值范围在数轴上表示为(■).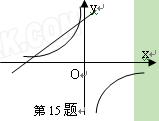
过反比例函数y=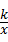 (k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足
(k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足 分别为B,C,如果△ABC的面积为3.则k的值为_________.
分别为B,C,如果△ABC的面积为3.则k的值为_________.
小明乘车从南充到成都,行车的平均速度v(km/h)和行车时间t(h)之间的函数图象是( )
如图,已知点A的坐标为( ,3),AB⊥x轴,垂足为B,连接OA,反比例函数
,3),AB⊥x轴,垂足为B,连接OA,反比例函数

(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的 倍的长为半径作圆,则该圆与x轴的位置关系是 (填“相离”、“相切”或“相交”).
倍的长为半径作圆,则该圆与x轴的位置关系是 (填“相离”、“相切”或“相交”).
若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=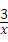 图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系正确的是( )
图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系正确的是( )
| A.y3>y1>y2 | B.y1>y2>y3 |
| C.y2>y1>y3 | D.y3>y2>y1 |
若点A(m,﹣2)在反比例函数 的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .
的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .
如图,已知直线AB与x轴交于点C,与双曲线 交于A(3,
交于A(3, )、B(﹣5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
)、B(﹣5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).
(1)求点D的坐标;
(2)求经过点C的反比例函数解析式.
如图是我们学过的反比例函数图象,它的函数解析式可能是( )
A. |
B. |
C. |
D. |
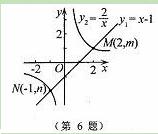
如图,函数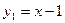 和函数
和函数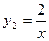 的图像相交于点M(2,
的图像相交于点M(2,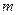 ),N(-1,
),N(-1,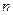 ),
),
若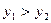 ,则
,则 的取值范围是
的取值范围是
A.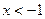 或 或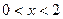 |
B.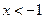 或 或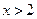 |
C.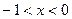 或 或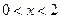 |
D.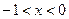 或 或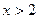 |
(11·西宁)反比例函数y= 的图象如图5所示,则k的值可能是
的图象如图5所示,则k的值可能是
| A.-1 | B. | C.1 | D.2 |

(本题6分) (湖南湘西,22,6分)如图,已知反比例函数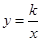 的图象经过点A(1,2).
的图象经过点A(1,2).
(1)求k的值.
(2)过点A分别作x轴和y轴的垂线,垂足为B和C,求矩形ABOC的面积.