如图, 在同一坐标系中(水平方向是x轴),函数 和
和 的图象大致是
的图象大致是 
下列关于反比例函数的叙述,不正确的是
A.反比例函数y= 的图象绕原点旋转180°后,能与原来的图象重合; 的图象绕原点旋转180°后,能与原来的图象重合; |
B.反比例函数y= 的图象既不与x轴相交,也不与y轴相交; 的图象既不与x轴相交,也不与y轴相交; |
C.经过反比例函数y= 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于 ; ; |
D.反比例函数y= ,当k>0时,y随x的增大而减少。 ,当k>0时,y随x的增大而减少。 |
反比例函数y= (k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直
(k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直
x轴于点P,如果△MOP的面积为1,那么k的值是
| A.1 | B.2 | C.4 | D. |
如图,过y轴上点A的一次函数与反比例函数相交于B、D两点,B(﹣2,3),BC⊥x轴于C,四边形OABC面积为4.
(1)求反比例函数和 一次函数的解析式;
一次函数的解析式;
(2)求点D的坐标;
(3)当x在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)
如图,已知反比例函数 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(﹣4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO= (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
已知点P(﹣1,4)在反比例函数 的图象上,则k的值是( )
的图象上,则k的值是( )
A.  |
B. |
| C.4 | D.﹣4 |
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数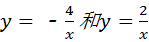 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
| A.3 | B.4 |
| C.5 | D.6 |
在Rt△ABC中,∠C=90°,∠A=30°,BC=2.若将此直角三角形的一条直角边BC或AC与x轴重合,使点A或点B刚好在反比例函数 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示) D是斜边与y轴的交点,通过计算比较S1、S2的大小.
D是斜边与y轴的交点,通过计算比较S1、S2的大小.
如图所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为 .
已知点A(2,3)在反比例函数 的图象上,则k的值是( )
的图象上,则k的值是( )
| A.﹣7 | B.7 |
| C.﹣5 | D.5 |
码头工人以每天40吨的速度往一艘轮船上装卸货物,装载完毕恰好用8天时间。
(1)轮船到达目的地后开始卸货,卸货速度为v(单位:吨/天),卸货时间为t(单位:天),求出v与t的函数关系式;
(2)由于遇到紧急情况,船上的货物必须在不超过5天内卸载完毕,那么平均每天至少要卸多少吨货物?