问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
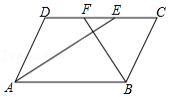
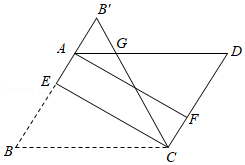
小丽在"红色研学"活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的"奔跑者"形象来激励自己.已知图1正方形纸片的边长为4,图2中 ,则"奔跑者"两脚之间的跨度,即 , 之间的距离是 .
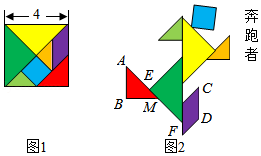
如图,矩形 中, , ,点 是 边上一点, ,连接 ,点 是 延长线上一点,连接 ,且 ,则 .
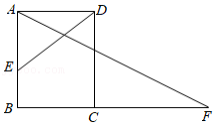
如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
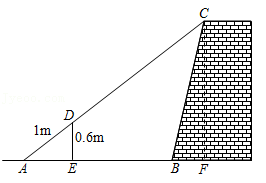
如图,在平行四边形 中, ,点 为线段 的三等分点(靠近点 ,点 为线段 的三等分点(靠近点 ,且 .将 沿 对折, 边与 边交于点 ,且 .
(1)证明:四边形 为矩形;
(2)求四边形 的面积.
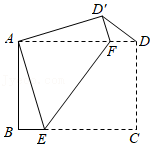
如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
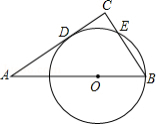
如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
1 |
如图,已知线段 , ,垂足为 .
(1)求作四边形 ,使得点 , 分别在射线 , 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 , 分别为(1)中四边形 的边 , 的中点,求证:直线 , , 相交于同一点.

如图,在 中, , , ,以点 为圆心,2为半径的圆与 交于点 ,过点 作 交 于点 ,点 是边 上的动点.当 最小时, 的长为
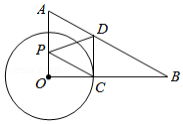
A. B. C.1D.
如图,经过原点 的直线与反比例函数 的图象交于 , 两点(点 在第一象限),点 , , 在反比例函数 的图象上, 轴, 轴,五边形 的面积为56,四边形 的面积为32,则 的值为 , 的值为 .
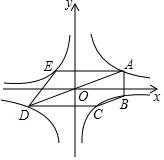
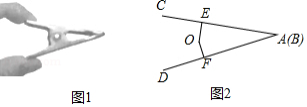
图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为 , (点 与点 重合),点 是夹子转轴位置, 于点 , 于点 , , , , .按图示方式用手指按夹子,夹子两边绕点 转动.
(1)当 , 两点的距离最大时,以点 , , , 为顶点的四边形的周长是 .
(2)当夹子的开口最大(即点 与点 重合)时, , 两点的距离为 .
如图, 中, , 是 的外接圆, 的延长线交边 于点 .
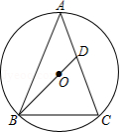
[小题1]求证: ;
[小题2]当 是等腰三角形时,求 的大小;
[小题3]当 , 时,求边 的长.
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
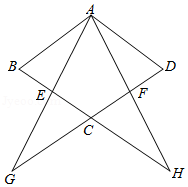
[小题1]求证: ;
[小题2]如果 ,求证: .