如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形, 经过点 ,连接 交 于点 ,观察发现:点 是 的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接 交 于点 .
请参考上面的思路,证明点 是 的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当 时,延长 、 交于点 ,求 的值;
(3)在(2)的条件下,若 为大于 的常数),直接用含 的代数式表示 的值.

如图, 是平面直角坐标系中第四象限内一点,过点 作 轴于点 ,以 为斜边在右侧作等腰 ,已知直角顶点 的纵坐标为 ,连接 交 于 , .
(1)求点 的坐标;
(2)连接 ,求 的面积与 的面积之比.
如图, 是平面直角坐标系中第四象限内一点,过点 作 轴于点 ,以 为斜边在右侧作等腰 ,已知直角顶点 的纵坐标为 ,连接 交 于 , .
(1)求点 的坐标;
(2)连接 ,求 的面积与 的面积之比.
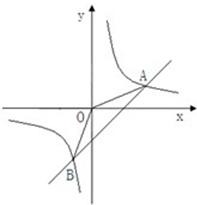
如图,一次函数y=kx+b(k≠0)的图象过点P(﹣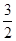 ,0),且与反比例函数
,0),且与反比例函数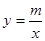 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.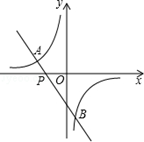
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
(本小题满分6分)如图,将透明三角形纸片PAB的直角顶点P落在第二象限,顶点A、B分别落在反比例函数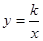 图象的两支上,且PB⊥y轴于点C,PA⊥x轴于点D,AB分别与x轴、y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥y轴于点C,PA⊥x轴于点D,AB分别与x轴、y轴相交于点E、F.已知B(1,3).
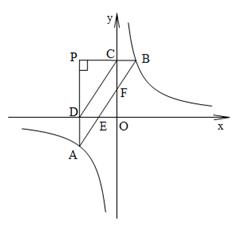
(1)k=__ _;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为4时,直接写出点P的坐标.
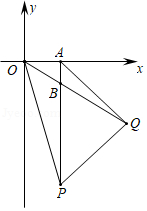
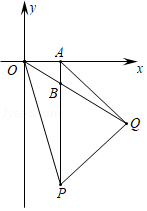
如图,已知点A、P在反比例函数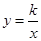 (
(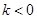 )的图象上,点B、Q在直线
)的图象上,点B、Q在直线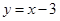 的图象上,点B的纵坐标为﹣1,AB⊥x轴,且
的图象上,点B的纵坐标为﹣1,AB⊥x轴,且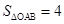 ,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
,若P、Q两点关于y轴对称,设点P的坐标为(m,n).
(1)求点A的坐标和k的值;
(2)求 的值.
的值.
(本小题7分)如图,一次函数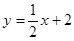 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数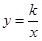 的图象的一个交点为A(2,m).
的图象的一个交点为A(2,m).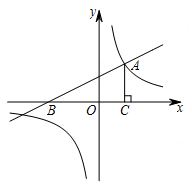
(1)求反比例函数的表达式;
(2)求当x满足什么范围时, <
< ;
;
(3)过点A作AC⊥x轴,垂足为点C,如果求点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
如图平面直角坐标系中,点A(1,n)和点B(m,1)为双曲线y= 第一象限上两点,连结OA、OB.
第一象限上两点,连结OA、OB.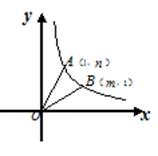
(1)试比较m、n的大小;
(2)若∠AOB=30°,求双曲线的解析式.
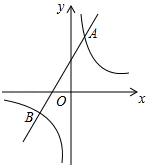
如图,已知反比例函数 的图象与一次函数
的图象与一次函数 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,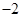 ).
).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图像与反比例函数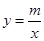 (m≠0)的图像交于A,B两点,与x轴交于点C,点A的坐标为(n,6),点C的坐标为(-2,0)且tan∠ACO=2.
(m≠0)的图像交于A,B两点,与x轴交于点C,点A的坐标为(n,6),点C的坐标为(-2,0)且tan∠ACO=2.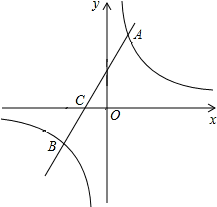
(1)求反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形(直接写出点E的坐标)
如图,一次函数 的图象与反比例函数
的图象与反比例函数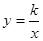 的图象交于
的图象交于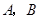 两点,与
两点,与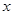 轴交于点
轴交于点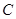 ,与
,与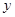 轴交于点
轴交于点 ,已知
,已知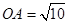 ,
,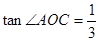 ,点
,点 的坐标为
的坐标为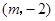 .
.
(1)求反比例函数的解析式.
(2)求一次函数的解析式.
(3)在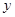 轴上存在一点
轴上存在一点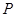 ,使得
,使得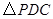 与
与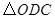 相似,请你求出
相似,请你求出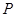 点的坐标.
点的坐标.
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=的图象的两个交点.
求此反比例函数和一次函数的解析式
根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
如图,一次函数的图象与反比例函数y1=-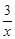 (x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值
(x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值
求一次函数的解析式
设函数y2=
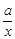 (x>0)的图象与y1=-
(x>0)的图象与y1=-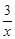 (x<0)的图象关于y轴对称,在y2=
(x<0)的图象关于y轴对称,在y2=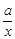 (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
(x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
、如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=﹣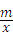 的图象的交点.
的图象的交点.
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.