如图,在矩形 中, , , 是 边上一点,沿 折叠 ,使点 恰好落在 边上的 处, 是 的中点,连接 ,则 .
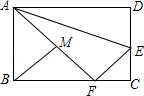
如图,在矩形 中, , ,将矩形 沿 折叠,点 落在 处,若 的延长线恰好过点 ,则 的值为 .

如图,三角形纸片 , , ,点 为 中点.沿过点 的直线折叠,使点 与点 重合,折痕 交 于点 .已知 ,则 的长是

A. B. C.3D.
如图,将一张三角形纸片 的一角折叠,使点 落在 外的 处,折痕为 .如果 , , ,那么下列式子中正确的是

A. B. C. D.
如图1,一个扇形纸片的圆心角为 ,半径为6.如图2,将这张扇形纸片折叠,使点 与点 恰好重合,折痕为 ,图中阴影为重合部分,则阴影部分的面积为

A. B. C. D.
再读教材:
宽与长的比是 (约为 的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:
第一步,在矩形纸片一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.

第三步,折出内侧矩形的对角线 ,并把 折到图③中所示的 处.
第四步,展平纸片,按照所得的点 折出 ,使 ,则图④中就会出现黄金矩形.

问题解决:
(1)图③中 (保留根号);
(2)如图③,判断四边形 的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
实际操作
(4)结合图④,请在矩形 中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
如图,把正方形纸片 沿对边中点所在的直线对折后展开,折痕为 ,再过点 折叠纸片,使点 落在 上的点 处,折痕为 .若 的长为2,则 的长为

A.2B. C. D.1
如图,将一张矩形纸片 的边 斜着向 边对折,使点 落在 上,记为 ,折痕为 ;再将 边斜向下对折,使点 落在 边上,记为 ,折痕为 , , .则矩形纸片 的面积为 .

如图,四边形 为一个矩形纸片, , ,动点 自 点出发沿 方向运动至 点后停止, 以直线 为轴翻折,点 落在点 的位置.设 ,△ 与原纸片重叠部分的面积为 .

(1)当 为何值时,直线 过点 ?
(2)当 为何值时,直线 过 的中点 ?
(3)求出 与 的函数表达式.
实验探究:
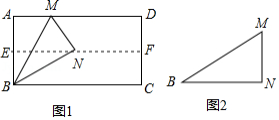
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
如图1,在矩形纸片 中, , ,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 、 也随之移动;
①当点 与点 重合时(如图 ,求菱形 的边长;
②若限定 、 分别在边 、 上移动,求出点 在边 上移动的最大距离.

如图,将矩形 沿 对折,点 落在 处,点 落在 边上的 处, 与 相交于点 ,若 , , ,则 周长的大小为 .

如图, 为 的 边上的中线,沿 将 折叠, 的对应点为 ,已知 , ,那么点 与 的距离为

A.3B. C. D.4
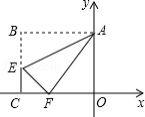
如图,在平面直角坐标系中,矩形 的边 、 分别在 轴、 轴上,点 在边 上,将该矩形沿 折叠,点 恰好落在边 上的 处.若 , ,则点 的坐标是 .