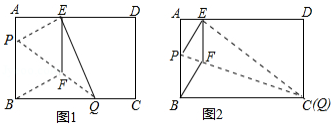
如图1，在矩形纸片 中， ， ，折叠纸片使 点落在边 上的 处，折痕为 ，过点 作 交 于 ，连接 ．
（1）求证：四边形 为菱形；
（2）当点 在 边上移动时，折痕的端点 、 也随之移动；
①当点 与点 重合时（如图 ，求菱形 的边长；
②若限定 、 分别在边 、 上移动，求出点 在边 上移动的最大距离．
在线段
上，
是等边三角形．（1）当
满足怎样的关系式时
；（2）当
的度数．
中，
是
上的一点，
，在
上是否存在一点
，使
三点组成的三角形与
的长；如果不存在，请说明理由．
分别为边
的三等分点（即：
），若
，求
的大小．
为
的中点，求
的周长．
若
cm，
cm，试求
的长．
相关知识点
推荐套卷
如图1，在矩形纸片 中， ， ，折叠纸片使 点落在边 上的 处，折痕为 ，过点 作 交 于 ，连接 ．
（1）求证：四边形 为菱形；
（2）当点 在 边上移动时，折痕的端点 、 也随之移动；
①当点 与点 重合时（如图 ，求菱形 的边长；
②若限定 、 分别在边 、 上移动，求出点 在边 上移动的最大距离．
粤公网安备 44130202000953号