初中数学圆内接四边形的性质试题

如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C. 则A′C长度的最小值是       .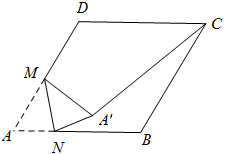

(9分)如图所示，在边长为1的正方形ABCD中，一直角三角尺PQR的直角顶点P在对角线AC上移动，直角边PQ经过点D，另一直角边与射线BC交于点E.
⑴试判断PE与PD的大小关系，并证明你的结论；
⑵连接PB，试证明：△PBE为等腰三角形；
⑶设AP＝x，△PBE的面积为y，
①求出y关于x 函数关系式；
②当点P落在AC的何处时，△PBE的面积最大，此时最大值是多少？

如图，在矩形中，点A的坐标是（-2，1），点C的纵坐标是4，则B、C两点的坐标为（  ）

A.（，）、（，）             B.（，）、（，）
C.(，)、（，）              D.(，) 、（，）

（本题6分）如图，四边形是正方形，点在上，，垂足为，请你在上确定一点，使，请你写出两种确定点G的方案，并写出其中一种方案的具体作法和证明．

方案

一：                                              ；

方案

二：（1）作法：

(2) 证明：

如图，在Rt△ABC中，∠B=90°，AC=60，AB=30。点D是AC上的动点，过D作DF⊥BC于F，再过F作FE//AC，交AB于E。设CD=x，DF=y.
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△FED是直角三角形时，求x的值.

如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N．
（1）①∠MPN=          ；
②求证：PM+PN=3a；
（2）如图2，点O是AD的中点，连接OM、ON，求证：OM=ON；
（3）如图3，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形？并说明理由．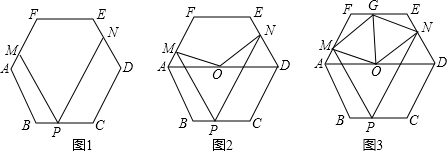

如图所示，直线与y轴交于点，以为边作正方形然后延长与直线交于点，得到第一个梯形；再以为边作正方形，同样延长与直线交于点得到第二个梯形；，再以为边作正方形，延长，得到第三个梯形；……则第2个
的面积是          ；第（n是正整数）个梯形的面积是           （用含n的式子
表示）．

如图，在边长为2的正方形ABCD中，G是AD延长线上的一点，且DG=AD，动点M从A出发，以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动（M不与A、G重合），设运动时间为t秒。连接BM并延长交AG于N。

（1）是否存在点M，使△ABM为等腰三角形？若存在，分析点M的位置；若不存在，请说明理由；
（2）当点N在AD边上时，若BN⊥HN，NH交∠CDG的平分线于H，求证：BN=NH；
（3）过点M分别用AB、AD的垂线，垂足分别为E、F，矩形AEMF与△ACG重叠部分的面积为S，求S的最大值。

认真阅读下列问题，并加以解决：
问题1：如图1，△ABC是直角三角形，∠C =90º．现将△ABC补成一个矩形．要求：使△ABC的两个顶点成为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．请将符合条件的所有矩形在图1中画出来；
            
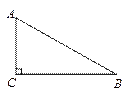
图1                                 图2 
问题2：如图2，△ABC是锐角三角形，且满足BC＞AC＞AB，按问题1中的要求把它补成矩形．请问符合要求的矩形最多可以画出      个，并猜想它们面积之间的数量关系是           （填写“相等”或“不相等”）；
问题3：如果△ABC是钝角三角形，且三边仍然满足BC＞AC＞AB，现将它补成矩形．要求：△ABC有两个顶点成为矩形的两个顶点，第三个顶点落在矩形的一边上,那么这几个矩形面积之间的数量关系是           （填写“相等”或“不相等”）．

如图，菱形ABCD中，AB=4，∠ABC=60°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为           .

已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点（不与B、C重合），过F点的反比例函数（k＞0）的图象与AC边交于点E.
（1）求证：△AOE与△BOF的面积相等.
（2）记S＝S_△OEF－S_△ECF，求当k为何值时，S有最大值，最大值为多少？
（3）请探索：是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存
在，请直接写出点F的坐标，若不存在，请说明理由.

如图（2），正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD + PE的最小值为                 .

如图所示，正方形的面积为12，是等边三角形，点在正方形
内，在对角线上有一点，使的和最小，则这个最小值为       .

如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．
（1）求AD的长；
（2）BC是⊙O的切线吗？若是，给出证明；若不是，说明理由．

如图，正方形的边长为2，以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；然后以为对角线作正方形，又以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；…，按此规律继续作下去，设弧与边、围成的阴影部分面积为．则：（1）=      ；（2）=      ．