[安徽]2014年初中毕业升学考试(安徽卷)数学
某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如右表,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )
| 棉花纤维长度x |
频数 |
| 0≤x<8 |
1 |
| 8≤x<16 |
2 |
| 16≤x<24 |
8 |
| 24≤x<32 |
6 |
| 32≤x<40 |
3 |
A.0.8 B.0.7 C.0.4 D.0.2
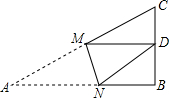
如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.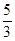 |
B.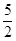 |
C.4 | D.5 |
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )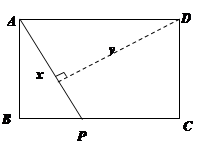
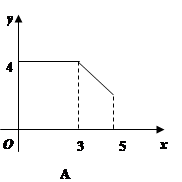
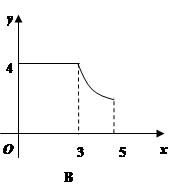
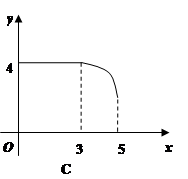
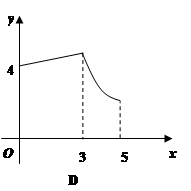
如图,正方形ABCD的对角线BD长为2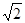 ,若直线l满足:(1)点D到直线l的距离为
,若直线l满足:(1)点D到直线l的距离为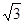 ,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
A.1 B.2 C.3 D.4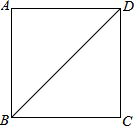
某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y= .
如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=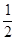 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF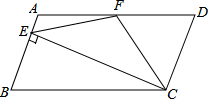
观察下列关于自然数的等式:
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式:92—4×( )2=( );
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
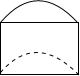
如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”。
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2—4mx+2m2+1,和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值。




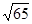 <n+1,则n的值为( )
<n+1,则n的值为( )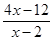 =3的解是x= .
=3的解是x= . .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号