初中数学圆内接四边形的性质试题

在矩形ABCD中，，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．
（1）如图1，当DH=DA时，
①填空：∠HGA=       度；
②若EF∥HG，求∠AHE的度数，并求此时a的最小值；
（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

在菱形ABCD和正三角形BGF中，∠ABC=60°，P是DF的中点，连接PG、PC．
（1）如图1，当点G在BC边上时，易证：PG=PC．（不必证明）
（2）如图2，当点F在AB的延长线上时，线段PC、PG有怎样的数量关系，写出你的猜想，并给与证明；
（3）如图3，当点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，写出你的猜想（不必证明）．

如图，在矩形ABCD中，AB=3，BC=4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P作PE∥DC，交AC于点E，动点P、Q的运动速度是每秒1个单位长度，运动时间为t秒，当点P运动到点A时，P、Q两点同时停止运动．

（1）用含有t的代数式表示PE=           ；
（2）探究：当t为何值时，四边形PQBE为梯形？
（3）是否存在这样的点P和点Q，使△PQE为等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

（本题8分）在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动，同时点Q从点B出发，以每秒1个单位的速度沿BA向终点A运动，设运动时间为t秒.
⑴当t为何值时，四边形PQBC为平行四边形时？
⑵在整个运动过程中，当t为何值时，以点C、P、Q为顶点的三角形是直角三角形？

 

如图，在边长为4的正方形ABCD中，动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动，动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动，动点E比动点F先出发1秒，其中一个动点到达终点时，另一个动点也随之停止运动，设点F的运动时间为t秒．

（1）点F在边BC上．
①如图1，连接DE，AF，若DE⊥AF，求t的值；
②如图2，连结EF，DF，当t为何值时，△EBF与△DCF相似？
（2）如图3，若点G是边AD的中点，BG，EF相交于点O，试探究：是否存在在某一时刻t，使得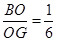？若存在，求出t的值；若不存在，请说明理由．

如图，在平行四边形ABCD中，平分，交于点，平分，交于点，与交于点，连接，.
（1）求证：四边形是菱形；
（2）若，，，求的值.

如图，菱形ABCD中，点E,M在A,D上，且CD=CM，点F为AB上的点，且∠ECF=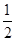∠B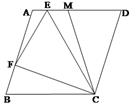

（1）若菱形ABCD的周长为8，且∠D=67.5°，求△MCD的面积。
（2）求证：BF=EF-EM

如图，若长方形APHM,BNHP,CQHN的面积分别为7、4、6，求阴影部分的面积是多少？

阅读下面材料：
在学习小组活动中，小明探究了下面问题：菱形纸片ABCD的边长为2，折叠菱形纸片，将B、D两点重合在对角线BD上的同一点处，折痕分别为EF、GH．当重合点在对角线BD上移动时，六边形AEFCHG的周长的变化情况是怎样的？
小明发现：若∠ABC=60°，
①如图1，当重合点在菱形的对称中心O处时，六边形AEFCHG的周长为_________；
②如图2，当重合点在对角线BD上移动时，六边形AEFCHG的周长_________（填“改变”或“不变”）.
请帮助小明解决下面问题：
如果菱形纸片ABCD边长仍为2，改变∠ABC的大小，折痕EF的长为m．
（1）如图3，若∠ABC=120°，则六边形AEFCHG的周长为_________；
（2）如图4，若∠ABC的大小为，则六边形AEFCHG的周长可表示为________．

如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点， DFAC于F．
（1）求证：DF为⊙O的切线；
（2）若，CF=9，求AE的长．

如图1，已知△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点．作正方形DEFG，使点A、C分别在DG和DE上，连接AE，BG．
（1）试猜想线段BG和AE的数量关系是           ；
（2）将正方形DEFG绕点D逆时针方向旋转α（0°＜α≤360°），
①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；
②若BC=DE=4，当AE取最大值时，求AF的值．

四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF，连接DF，G为DF的中点，连接EG，CG，EC．
（1）如图1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及的值；
（2）将图1中的△BEF绕点B顺时针旋转至图2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；
（3）将图1中的△BEF绕点B顺时针旋转α（0°＜α＜90°），若BE=1，，当E，F，D三点共线时，求DF的长及tan∠ABF的值．

如图9四边形ABCD是菱形，且，是等边三角形，M为对角线BD(不含B点)上任意一点，将BM绕点B逆时针旋转得到BN，连接EN、AM、CM，则下列五个结论中正确的是（   ）

①若菱形ABCD的边长为1,则的最小值1;
②；
③；④连接AN，则；
⑤当的最小值为时，菱形ABCD的边长为2.

A．①②③

B．②④⑤

C．①②⑤

D．②③⑤

若从矩形一边上的点到对边的视角是直角，即称该点是直角点。例如，如图的矩形中，点在边上，连接，,则点为直角点。若点分别为矩形的边上的直角点，且,,则的长为     

在矩形ABCD中，已知AB=2cm，BC=3cm，现有一根长为2 cm的木棒EF紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则木棒EF的中点P在运动过程中所围成的图形的面积为（ ）

A．6 cm^2

B．3 cm^2

C．（2＋π）cm^2

D．（6－π）cm^2