两组邻边分别相等的四边形我们称它为筝形.
如图,在筝形 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,
(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求筝形
,求筝形 的面积.
的面积.
如图所示,把长方形ABCD的纸片,沿EF线折叠后,ED与BC的交点为G,点D、C分别落在D/、C/的位置上,若∠1=70°,求∠2、∠EFG的度数.
在矩形 中,
中, ,
, ,点
,点 从点
从点 沿矩形的边以
沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 从
从 点出发沿矩形的边以
点出发沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 、
、 同时运动,且一点到达终点另一点也停止运动,求几秒后以
同时运动,且一点到达终点另一点也停止运动,求几秒后以 、
、 、
、 为顶点的三角形的面积等于6平方厘米?
为顶点的三角形的面积等于6平方厘米?
如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE= ,则AE= .
,则AE= .
如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE满足什么条件时,四边形BEDF是菱形,说明理由.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论;
(2)若AB=13,AC=10,请求出线段EF的长.
已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
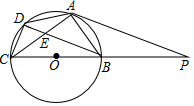
如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.