[江苏]2013届江苏省扬州市邗江区九年级下学期期中(一模)考试数学试卷
聪聪同学在“百度”搜索引擎中输入“圆”,能搜索到与之相关的结果个数约为100000000,这个数用科学记数法表示为
| A.1×107 | B.1×108 | C.10×107 | D.10×108 |
本学期的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为1.2、0.5,由此可知( )
| A.甲比乙的成绩稳定 | B.乙比甲的成绩稳定 |
| C.甲乙两人的成绩一样稳定 | D.无法确定谁的成绩更稳定 |
下列函数的图像在其所在的每一个象限内,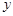 值随
值随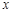 值的增大而增大的是( )
值的增大而增大的是( )
A.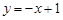 |
B.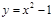 |
C.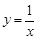 |
D.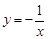 |
如图,△ABC的顶点是正方形网格的格点,则sinA的值为( )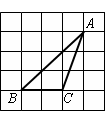
A.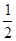 |
B.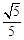 |
C.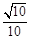 |
D.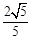 |
一张圆形纸片,小芳进行了如下连续操作:
⑴.将圆形纸片左右对折,折痕为AB,如图(2)所示.
⑵.将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图(3)所示.
⑶.将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图(4)所示.
⑷.连结AE、AF,如图(5)所示.
经过以上操作小芳得到了以下结论:①. CD∥EF ②.四边形MEBF是菱形
③. △AEF为等边三角形 ④. ,以上结论正确的有( )
,以上结论正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在⊙O中,直径CD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB= ,则∠BCD= 度.
,则∠BCD= 度.
秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡秋千在最高处踩板离地面2米(左右对称),则该秋千所荡过的圆弧长为 米.
已知二次函数 中函数
中函数 与自变量
与自变量 之间的部分对应值如下表所示,点
之间的部分对应值如下表所示,点 、
、 在函数图象上,当
在函数图象上,当 时,则
时,则
 (填“
(填“ ”或“
”或“ ”).
”).
 |
|
0 |
1 |
2 |
3 |
|
 |
|
 |
2 |
3 |
2 |
|
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 的图象上。若点A的坐标为(-3,-3),则
的图象上。若点A的坐标为(-3,-3),则 的值为 .
的值为 .
两组邻边分别相等的四边形我们称它为筝形.
如图,在筝形 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,
(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求筝形
,求筝形 的面积.
的面积.
课外兴趣小组为了解某段路上机动车的车速,抽查了一段时间内若干辆车的车速(车速取整数,单位:千米/时)并制成如图所示的频数分布直方图.已知车速在41千米/时到50千米/时的车辆数占车辆总数的 .
.
(1)在这段时间中他们抽查的车有 辆;
(2)被抽查车辆的车速的中位数所在速度段(单位:千米/时)是( )
| A.30.5~40.5 | B.40.5~50.5 | C.50.5~60.5 | D.60.5~70.5 |
(3)补全频数分布直方图,并在图中画出频数折线图;
(4)如果全天超速(车速大于60千米/时)的车有240辆,则当天的车流量约为多少辆?
一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,
点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距
离(精确到1cm).(参考数据: )
)
某楼盘准备以每平方米6000元的均价对外销售,由于购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售。
(1)求平均每次下调的百分率。
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
在△ABC中,∠C=90°,AC=6cm,BC=8cm,扇形ODF与BC边相切,切点是E,若FO⊥AB于点O.求扇形ODF的半径.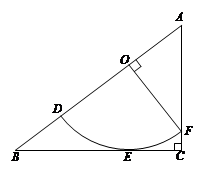
爸爸、妈妈和小明一家三人准备在下周六每人骑一辆车出行,家里有三辆车:自行车1、自行车2和电瓶车,小明只能骑自行车,爸爸、妈妈可以骑任意一辆车.
(1)请列举出他们出行有哪几种骑车方案;
(2)如果下周日三人继续这样每人骑一辆车出行,请用列表或画树状图的方法计算两次出行骑车方案相同的概率.(为了便于描述,骑车方案一、方案二 可以分别用 、
、 来表示)
来表示)
小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
(1)A点所表示的实际意义是 ; = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?




 的相反数是 .
的相反数是 . 有意义的条件是 .
有意义的条件是 . = .
= . ,则代数式
,则代数式 的值是 .
的值是 . cm2,则这个圆锥的高为 cm..
cm2,则这个圆锥的高为 cm.. (2)解方程组:
(2)解方程组: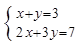 .
. ,求
,求 的值.
的值.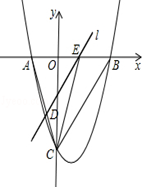
 粤公网安备 44130202000953号
粤公网安备 44130202000953号