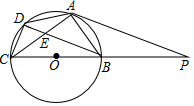
如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
如图,在平面直角坐标系中,四边形 是以 为直径的 的内接四边形,点 , 在 轴上, 是边长为2的等边三角形,过点 作直线 与 轴垂直,交 于点 ,垂足为点 ,且点 平分 .
(1)求过 , , 三点的抛物线的解析式;
(2)求证:四边形 是菱形;
(3)请问在抛物线上是否存在一点 ,使得 的面积等于定值5?若存在,请求出所有的点 的坐标;若不存在,请说明理由.

已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
如图,E是矩形ABCD的边CD上的一点,BE交AC于点O,已知△OCE和△OBC的面积分别为2和8.
(1)求△OAB和四边形AOED的面积;
(2)若BE⊥AC,求BE的长.
如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
(本小题满分10分)如图,在四边形ABCD中,AD∥BC,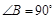 ,AD=8cm,BC=10cm,
,AD=8cm,BC=10cm,
AB=6cm,,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(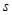 ).
).
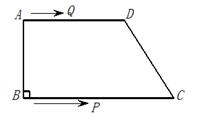
(1)直接写出:QD= ,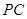 = ;(用含t的式子表示)
= ;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当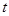 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
(本小题满分8分)如图,在正方形ABCD中,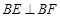 ,
,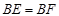 ,EF交BC于点G.
,EF交BC于点G.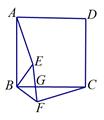
(1)求证: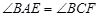 ;
;
(2)若 ,求
,求 的大小.
的大小.