江苏省扬州市仪征市九年级上学期期中数学试卷
关于x的一元二次方程x2﹣2ax﹣1=0(其中a为常数)的根的情况是( )
| A.有两个不相等的实数根 |
| B.可能有实数根,也可能没有 |
| C.有两个相等的实数根 |
| D.没有实数根 |
如图,AB为⊙O的直径,点C在⊙O上,∠A=40°,则∠B的度数为( )

| A.20° | B.40° | C.50° | D.60° |
下列命题:①直径是圆中最长的弦; ②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④菱形的四个顶点在同一个圆上;其中正确结论的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
在▱ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )

| A.1:2 | B.1:3 | C.2:3 | D.2:5 |
要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A. x(x+1)=28 x(x+1)=28 |
B. x(x﹣1)=28 x(x﹣1)=28 |
| C.x(x+1)=28 |
| D.x(x﹣1)=28 |
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )
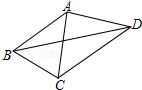
| A.110° | B.88° | C.84° | D.66° |
⊙O的半径为R,圆心O到点A的距离为d,且R、d分别是方程x2﹣6x+9=0的两根,则点A与⊙O的位置关系是 .
在如图所示的平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,则圆心P的坐标是 .
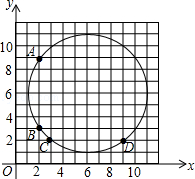
一块矩形菜地的面积是120平方米,如果它的长减少2米,那么菜地就变成了正方形,则原矩形的长是 米.
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)若1是该方程的一个根.求m的值并求出此时方程的另一个根.
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
如图△ABC中,DE∥BC,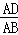 =
=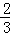 ,M为BC上一点,AM交DE于N.
,M为BC上一点,AM交DE于N.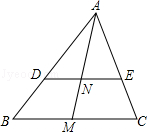
(1)若AE=4,求EC的长;
(2)若M为BC的中点,S△ABC=36,求S△ADN.
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.
(1)求⊙O的半径;
(2)求证:CE=BE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若∠B=70°,求弧DE的度数.
(3)若BD=2,BE=3,求AC的长.
如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).

(1)若点A在优弧 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.






 = .
= .

 +
+ = .
= .
 ,
, ,求AB的值.
,求AB的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号