北京市海淀区中考一模数学试卷
据教育部通报,2014年参加全国硕士研究生入学考试的人数约为1720000.数字1720000用科学记数法表示为( )
A. |
B. |
C. |
D. |
一个不透明的盒子中放有4个白色乒乓球和2个黄色乒乓球,所有乒乓球除颜色外完全相同,从中随机摸出1个乒乓球,摸出黄色乒乓球的概率为( )
A. |
B. |
C. |
D. |
下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差
与方差 :
:
| |
甲 |
乙 |
丙 |
丁 |
平均数 (cm) (cm) |
561 |
560 |
561 |
560 |
方差 (cm2) (cm2) |
3.5 |
3.5 |
15.5 |
16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
如图,在 ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
| A.150° | B.130° | C.120° | D.100° |
如图,点P是以O为圆心, AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C、D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.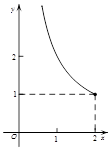 B.
B.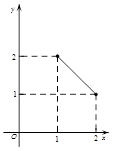 C.
C.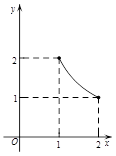 D.
D.
如图,矩形台球桌ABCD的尺寸为2.7m 1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.
1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.
在一次数学游戏中,老师在 三个盘子里分别放了一些糖果,糖果数依次为
三个盘子里分别放了一些糖果,糖果数依次为 ,
, ,
, ,记为
,记为 (
( ,
, ,
, ).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.
).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束. 次操作后的糖果数记为
次操作后的糖果数记为 (
( ,
, ,
, ).
).
(1)若 (4,7,10),则第_______次操作后游戏结束;
(4,7,10),则第_______次操作后游戏结束;
(2)小明发现:若 (4,8,18),则游戏永远无法结束,那么
(4,8,18),则游戏永远无法结束,那么 ________.
________.
如图,在△ABC中,∠ACB=90º, D是AC上的一点,且AD=BC,DE AC于D,∠EAB=90º.
AC于D,∠EAB=90º.
求证:AB=AE.

列方程(组)解应用题:
某市计划建造80万套保障性住房,用于改善百姓的住房状况.开工后每年建造保障性住房的套数比原计划增加25%,结果提前两年保质保量地完成了任务.求原计划每年建造保障性住房多少万套?
如图,在平面直角坐标系 中,一次函数
中,一次函数 (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数 的图象相交于点B
的图象相交于点B ,
, .
.
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
如图,在△ABC中,∠ACB=90º,∠ABC=30º,BC= ,以AC为边在△ABC的外部作等边△ACD,连接BD.
,以AC为边在△ABC的外部作等边△ACD,连接BD.
(1)求四边形ABCD的面积;
(2)求BD的长.

社会消费品通常按类别分为:吃类商品、穿类商品、用类商品、烧类商品,其零售总额是反映居民生活水平的一项重要数据.为了了解北京市居民近几年的生活水平,小红参考北京统计信息网的相关数据绘制了统计图的一部分:
(1)北京市2013年吃类商品的零售总额占社会消费品零售总额的百分比为 ;
(2)北京市2013年吃类商品零售总额约为1673亿元,那么当年的社会消费品零售总额约为 亿元;请补全条形统计图,并标明相应的数据;
(3)小红根据条形统计图中的数据,绘制了北京市2010至2013年社会消费品零售总额年增长率统计表(如下表),其中2013年的年增长率为 (精确到1%);请你估算,如果按照2013年的年增长率持续增长,当年社会消费品零售总额超过10000亿元时,最早要到 年(填写年份).
| 北京市2010至2013年社会消费品零售总额年增长率统计表 |
||||
| |
2010年 |
2011年 |
2012年 |
2013年 |
| 年增长率(精确到1%) |
17% |
11% |
12% |
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点, DF AC于F.
AC于F.
(1)求证:DF为⊙O的切线;
(2)若 ,CF=9,求AE的长.
,CF=9,求AE的长.
阅读下面材料:
在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,
①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为_________;
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长_________(填“改变”或“不变”).
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为_________;
(2)如图4,若∠ABC的大小为 ,则六边形AEFCHG的周长可表示为________.
,则六边形AEFCHG的周长可表示为________.



在平面直角坐标系 中,二次函数
中,二次函数 (
( )的图象与
)的图象与 轴正半轴交于A点.
轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为 ,且
,且 ,连接AD、BD.
,连接AD、BD.
(1)如图1,当∠BAC=100°, 时,∠CBD 的大小为_________;
时,∠CBD 的大小为_________;
(2)如图2,当∠BAC=100°, 时,求∠CBD的大小;
时,求∠CBD的大小;
(3)已知∠BAC的大小为m( ),若∠CBD 的大小与(2)中的结果相同,请直接写出
),若∠CBD 的大小与(2)中的结果相同,请直接写出 的大小.
的大小.

对于平面直角坐标系xOy中的点P(a,b),若点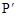 的坐标为(
的坐标为(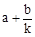 ,
,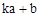 )(其中k为常数,且
)(其中k为常数,且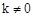 ),则称点
),则称点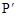 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为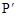 (1+
(1+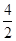 ,
,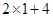 ),即
),即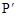 (3,6).
(3,6).
(1)①点P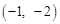 的“2属派生点”
的“2属派生点” 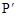 的坐标为____________;
的坐标为____________;
②若点P的“k属派生点” 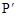 的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为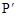 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;
(3)如图, 点Q的坐标为(0, ),点A在函数
),点A在函数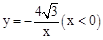 的图象上,且点A是点B的“
的图象上,且点A是点B的“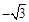 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.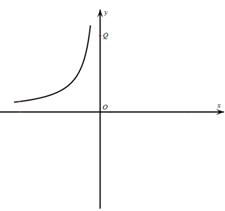
 的绝对值是( )
的绝对值是( )







 = .
= . 有两个不相等的实数根,则a的取值范围是_________.
有两个不相等的实数根,则a的取值范围是_________.

 .
.
 ,求代数式
,求代数式 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号