初中数学圆内接四边形的性质试题

（11·贺州）
如图，E、F是平行四边形ABCD对角线AC上的两点，BE∥DF．求证：BE＝DF．

（11·贺州）把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，
折痕为EF．若BF＝4，FC＝2，则∠DEF的度数是_   ▲   ．

（11·贺州）如图，在梯形ABCD中，AB∥CD，AB＝3CD，对角线AC、BD交
于点O，中位线EF与AC、BD分别交于M、N两点，则图中阴影部分的面积是梯形ABCD
面积的

如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB=6cm，AD=2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/ 秒的速度向终点B移动，点Q以1厘米/ 秒的速度向D移动，当有一点到达终点时，另一点也停止运动。设运动的时间为t ，问：
（1）当t=1秒时，四边形BCQP面积是多少？
（2）当t为何值时，点P和点Q距离是3cm？
（3）当t=     时， 以点P、Q、D为顶点的三角形是等腰三角形.（直接写出答案）

（11·佛山）阅读材料
我们经常通过认识一个事物的局部或其特殊类型，来逐步认识这个事物；
比如我们通过学习两类特殊的四边形，即平行四边形和梯形（继续学习它们的特殊类型如矩形、等腰梯形等）来逐步认识四边形；
我们对课本里特殊四边形的学习，一般先学习图形的定义，再探索发现其性质和判定方法，然后通过解决简单的问题巩固所学知识；
请解决以下问题：
如图，我们把满足AB＝CD、CB＝CD且AB≠BC的四边形ABCD叫做“筝形”；
（1）写出筝形的两个性质（定义除外）；
（2）写出筝形的两个判定方法（定义除外），并选出一个进行证明；

（11·佛山）在矩形ABCD中，两条对角线AC、BD相交于点O，若AB＝OB＝4，则AD＝ ；

（11·佛山）依次连接菱形的各边中点，得到的四边形是（              ）

A．矩形

B．菱形

C．正方形

D．梯形

如图，在□ABCD中，AC、BD相交于点O，点E是AB的中点．若OE＝3cm，则AD的长是       cm．

（本题8分）已知锐角△ABC中，边BC长为12，高AD长为8
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K

①求的值
②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值
（2）若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：
（1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.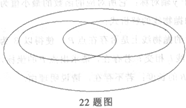

（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .
（3）某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a²，对此结论，你认为是否正确？若正确，请说明理由；若不正确，请举出一个反例说明.

在Rt△ABC中，∠C=90°，AC=3，BC=4，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是___________.

小明遇到这样一个问题：“如图1，在边长为a（a＞2）的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积．”
分析时，小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于 点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）
请回答：
（1）若将上述四个等腰直角三角形拼成一个正方形（无缝隙不重叠），则这个正方形的边长为_______
（2）求正方形MNPQ的面积．
（3）参考小明思 考问题的方法，解决问题：
如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ=，则AD的长为_______．

如图1，直线 $l:y=-\frac{3}{4}x+b$与 $x$轴交于点 $A(4,0)$，与 $y$轴交于点 $B$，点 $C$是线段 $\mathit{OA}$上一动点 $(0<\mathit{AC}<\frac{16}{5})$．以点 $A$为圆心， $\mathit{AC}$长为半径作 $\odot A$交 $x$轴于另一点 $D$，交线段 $\mathit{AB}$于点 $E$，连接 $\mathit{OE}$并延长交 $\odot A$于点 $F$．

（1）求直线 $l$的函数表达式和 $\tan \angle \mathit{BAO}$的值；

（2）如图2，连接 $\mathit{CE}$，当 $\mathit{CE}=\mathit{EF}$时，

①求证： $\mathit{\Delta OCE}\backsim \mathit{\Delta OEA}$；

②求点 $E$的坐标；

（3）当点 $C$在线段 $\mathit{OA}$上运动时，求 $\mathit{OE}\cdot \mathit{EF}$的最大值．

如图，D，E，F分别为△ABC三边的中点，则图中平行四边形的个数为　．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．