（本题8分）已知锐角△ABC中，边BC长为12，高AD长为8
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K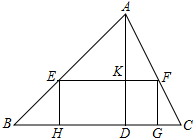
①求
的值
②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值
（2）若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．
相关试题
某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运，每辆汽车只能装运同一种救灾物资且必须装满，根据表中提供的信息，解答下列问题：
| 物资种类 |
食品 |
药品 |
生活用品 |
| 每辆汽车装载量（吨） |
6 |
5 |
4 |
| 每吨所需运费（元/吨） |
120 |
160 |
100 |
(1)设装运食品的车辆数为x，装运药品的车辆数为y，求y与x的函数关系式；
(2)如果装运食品和装运药品的车辆数均不少于4辆，求装运食品的车辆数x的取值范围；
(3)在（2）的条件下，若要求总运费最少，应如何安排车辆？并求出最少总运费．
已知点A（-4，n）和点B（2，-4）是反比例函数
的图象和一次函数
的图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求方程
的解（请直接写出答案）；
（3）求不等式
＞
的解集（请直接写出答案）.
（千米）关于时间
（小时）的函数图象如图所示.
相关知识点
推荐套卷
粤公网安备 44130202000953号