2011年初中毕业升学考试(广西贺州卷)数学
黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表
示为( )
| A.(11+t)℃ | B.(11-t)℃ | C.(t-11)℃ | D.(-t-11)℃ |
有如下图形:①函数 的图形;②函数
的图形;②函数 的图像;③一段弧;④平行
的图像;③一段弧;④平行
四边形,其中一定是轴对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
2010年12月份,某市总工会组织该市各单位参加“迎新春长跑活动”,将报名的
男运动员分成3组:青年组,中年组,老年组。各组人数所占比例如图(2)所示,已知青
年组有120人,则中年组与老年组人数分别是( )
| A.30,10 | B.60,20 | C.50,30 | D.60,10 |

将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. |
B.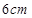 |
C.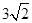  |
D. 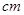 |

平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不
同的 个点最多可确定21条直线,则
个点最多可确定21条直线,则 的值为( )
的值为( )
A.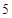 |
B. |
C.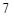 |
D.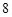 |
已知梯形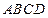 的四个顶点的坐标分别为
的四个顶点的坐标分别为 ,
, ,
, ,
,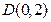 ,
,
直线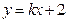 将梯形分成面积相等的两部分,则
将梯形分成面积相等的两部分,则 的值为( )
的值为( )
A. |
B. |
C.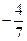 |
D. |
为响应“红歌唱响中国”活动,某乡镇举行了一场“红歌”歌咏比赛,组委会规
定:任何一名参赛选手的成绩 满足:
满足: ,赛后整理所有参赛选手的成绩如表(一)
,赛后整理所有参赛选手的成绩如表(一)
根据表(一)提供的信息得到 .
.
有甲、乙两张纸条,甲纸条的宽是乙纸条宽的2倍,如图(4)。将这两张纸条交
叉重叠地放在一起,重合部分为四边形 ,则
,则 与
与 的数量关系为 .
的数量关系为 .
初三年级某班有54名学生,所在教室有6行9列座位,用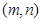 表示第
表示第 行第
行第 列的座位,新学期准备调整座位,设某个学生原来的座位为
列的座位,新学期准备调整座位,设某个学生原来的座位为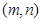 ,如果调整后的座位为
,如果调整后的座位为 ,则称该生作了平移[
,则称该生作了平移[ ]
] ,并称
,并称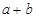 为该生的位置数。若某生的位
为该生的位置数。若某生的位
置数为 ,则当
,则当 取最小值时,
取最小值时,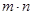 的最大值为 .
的最大值为 .
(本小题满分8分)2011年6月4日,李娜获得法网公开赛的冠军,圆了中国人
的网球梦,也在国内掀起一股网球热。某市准备为青少年举行一次网球知识讲座,小明和妹
妹都是网球球迷,要求爸爸去买门票,但爸爸只买回一张门票,那么谁去就成了问题,小明
想到一个办法:他拿出一个装有质地、大小相同的 个红球与
个红球与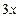 个白球的袋子,让爸爸摸
个白球的袋子,让爸爸摸
出一个球,如果摸出的是红球,妹妹去听讲座,如果摸出的是白球,小明去听讲座。
(1)爸爸说这个办法不公平,请你用概率的知识解释原因。
(2)若爸爸从袋中取出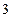 个白球,再用小明提出的办法来确定谁去听讲座,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
个白球,再用小明提出的办法来确定谁去听讲座,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
(本小题满分8分)东方山是鄂东南地区的佛教圣地,月亮山是黄荆山脉第二高峰,
山顶上有黄石电视塔。据黄石地理资料记载:东方山海拔453.20米,月亮山海拔442.00米,
一飞机从东方山到月亮山方向水平飞行,在东方山山顶 的正上方
的正上方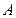 处测得月亮山山顶
处测得月亮山山顶 的
的
俯角为 ,在月亮山山顶
,在月亮山山顶 的正上方
的正上方 处测得东方山山顶
处测得东方山山顶 处的俯角为
处的俯角为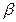 ,如图(7)。已知
,如图(7)。已知 ,若飞机的飞行速度为180米/秒,则该飞机从
,若飞机的飞行速度为180米/秒,则该飞机从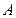 到
到 处
处
需多少时间?(精确到0.1秒)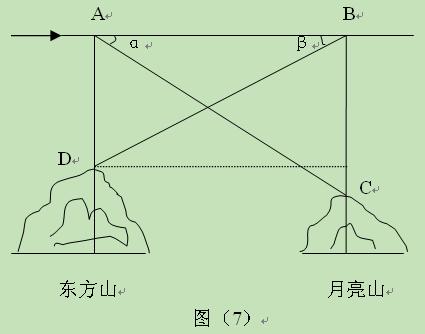
今年,号称"千湖之省"的湖北正遭受大旱,为提高学生环
境意识,节约用水,某校数学教师编制了一道应用题:为了保护水资源,某市制定一套节水
的管理措施,其中对居民生活用水收费作如下规定:
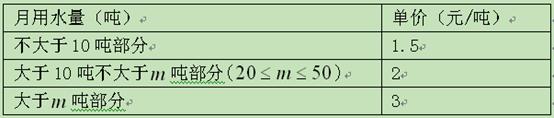
(1)若某用户六月份用水量为
吨,求其应缴纳的水费;
(2)记该用户六月份用水量为
吨,缴纳水费为
元,试列出
与
的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费
元的取值范围为
的取值范围。
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成。
(本小题满分9分)已知⊙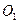 与⊙
与⊙ 相交于
相交于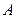 、
、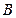 两点,点
两点,点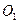 在⊙
在⊙ 上,
上, 为⊙
为⊙ 上一点(不与
上一点(不与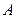 ,
,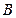 ,
,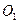 重合),直线
重合),直线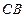 与⊙
与⊙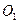 交于另一点
交于另一点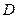 。
。
(1)如图(8),若 是⊙
是⊙ 的直径,求证:
的直径,求证: ;
;
(2)如图(9),若 是⊙
是⊙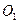 外一点,求证:
外一点,求证: ;
;
(3)如图(10),若 是⊙
是⊙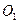 内一点,判断(2)中的结论是否成立。
内一点,判断(2)中的结论是否成立。
(本小题满分10分)已知二次函数
(1)当 时,函数值
时,函数值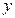 随
随 的增大而减小,求
的增大而减小,求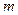 的取值范围。
的取值范围。
(2)以抛物线 的顶点
的顶点 为一个顶点作该抛物线的内接正三角形
为一个顶点作该抛物线的内接正三角形 (
( ,
,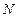 两点在抛物线上),请问:△
两点在抛物线上),请问:△ 的面积是与
的面积是与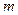 无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线 与
与 轴交点的横坐标均为整数,求整数
轴交点的横坐标均为整数,求整数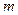 的值。
的值。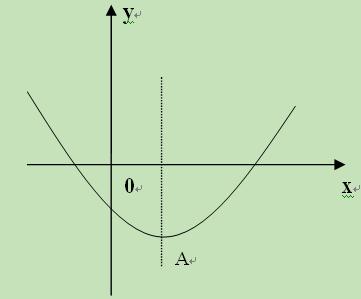
(11·贺州)国家统计局发布的第六次全国人口普查公报显示,我国总人口约为1
370 000 000人,1 370 000 000用科学记数法表示为
| A.13.7×108 | B.1.37×108 | C.1.37×109 | D.1.371×10-9 |
(11·贺州)在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球
1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件
| A.必然事件 | B.不可能事件 | C.随机事件 | D.确定事件 |
(11·贺州)已知⊙O1和⊙O2的半径分别为2和5,如果两圆的位置关系为外离,
那么圆心距O1O2的取值范围在数轴上表示正确的是
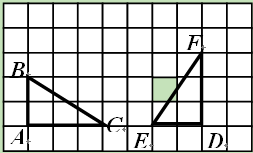
(11·贺州)如图,在方格纸中的△ABC经过变换得到△DEF,正确的变换是
| A.把△ABC向右平移6格, |
| B.把△ABC向右平移4格,再向上平移1格 |
| C.把△ABC绕着点A顺时针方向90º旋转,再右平移6格 |
| D.把△ABC绕着点A顺时针方向90º旋转,再右平移6格 |
(11·贺州)如图,在梯形ABCD中,AB∥CD,AB=3CD,对角线AC、BD交
于点O,中位线EF与AC、BD分别交于M、N两点,则图中阴影部分的面积是梯形ABCD
面积的

(11·贺州)在4张完全相同的卡片上分别画上图①、②、③、④.在看不见图
形的情况下随机抽取一张,卡片上的图形是中心对称图形的概率是 _ ▲ .
(11·贺州)把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,
折痕为EF.若BF=4,FC=2,则∠DEF的度数是_ ▲ .
(11·贺州)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1
次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,
按这样的运动规律,经过第2011次运动后,动点P的坐标是_ ▲ .
(本题满分10分,每小题5分)
(1)(11·贺州)
(2)(11·贺州)先化简,再求值:(a+1) (a-1)+a (1-a),其中a=2012.
(11·贺州)
如图,在平面直角坐标系中,点O为原点,反比例函数 的图象经过点(1,4),菱
的图象经过点(1,4),菱
形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
(11·贺州)
某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
(1)频数分布表中的m=_ ▲ ,n=_ ▲ ;
(2)样本中位数所在成绩的级别是_ ▲ ,扇形统计图中,E组所对应的扇形圆心角的度数是_ ▲ ;
(3)请你估计该校九年级的学生中,体育综合测试成绩不少于80分的大约有多少人?
(11·贺州)
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为2 000千克/亩、2 500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地收获两种生姜的年总产量为68 000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,
全部收购该基地生姜的年总收入最多?最多是多少元?
(11·贺州)
某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米);
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确
保安全 吗?
吗?
(参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.48,sin 58°12’≈0.85,tan 49°30’
≈1.17)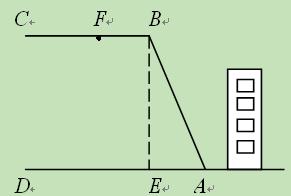
(11·贺州)
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线
交于点E.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
法);

 的图像经过第二、四象限,则
的图像经过第二、四象限,则 的取值范围是( )
的取值范围是( )
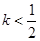



 的两根分别为
的两根分别为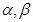 ,且
,且 ,则
,则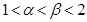


 且
且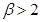
 = .
= . 内接于⊙
内接于⊙ ,若
,若 =30°,
=30°, ,则⊙
,则⊙
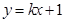 的图像与反比例函数
的图像与反比例函数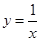 的图像没有公共点,则实数
的图像没有公共点,则实数 的
的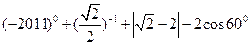
 ,其中
,其中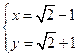 .
. 中,
中, ,
, ,
, 是
是 的中点,连接.
的中点,连接.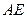 、
、 。求证:
。求证: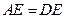 .
.









 与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,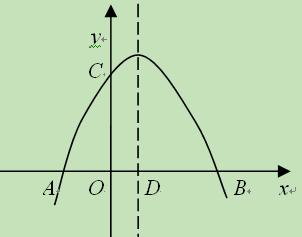
 粤公网安备 44130202000953号
粤公网安备 44130202000953号