[河南]2011届河南油田中招第一次模拟考试数学试卷
方程(x-5)(x-6)=x-5的解是 【 】
| A.x=5 | B.x=5或x=6 | C.x="7" | D.x=5或x=7 |
已知样本数据1,2,4,3,5,下列说法不正确的是 【 】
| A.平均数是3 | B.中位数是4 | C.极差是4 | D.方差是2 |
如图,已知矩形纸片 ,点
,点 是
是 的中点,点
的中点,点 是
是 上的一点,
上的一点, ,现沿直线
,现沿直线 将纸片折叠,使点
将纸片折叠,使点 落在纸片上的点
落在纸片上的点 处,连结
处,连结 ,则与
,则与 相等的角的个数为 【 】
相等的角的个数为 【 】 
| A.4 | B.3 | C.2 | D.1 |
如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),
半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是【 】 

A.2 B.1 C. D.
D.
某校举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年级各
有一名同学进入决赛,九年级有两名同学进入决赛.前两名都是九年级同学的概率是
如图,扇形的半径为6,圆心角 为120°,用这个扇形围成一个圆锥的侧面,
为120°,用这个扇形围成一个圆锥的侧面,
所得圆锥的底面半径为________.

如图,已知双曲线 经过直角三角形OAB斜边OB的中点D,与直角边
经过直角三角形OAB斜边OB的中点D,与直角边
AB相交于点C.若△OBC的面积为3,则k=_______.

如图所示,正方形 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点 在正方形
在正方形 内,在对角线
内,在对角线 上有一点
上有一点 ,使
,使 的和最小,则这个最小值为 .
的和最小,则这个最小值为 .

如图,已知BE⊥AD,CF⊥ AD,且BE=CF.
AD,且BE=CF.
(1)请你判断AD是△ABC的中线还是角平分线?证明你的结论.
(2)连接BF、CE,能否找到一个条件使四边形BFCE是菱形?直接写出答案: . (填“能”或“不能”)

农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了52个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
(1)请你在图1,图2中分别绘出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在5.5≤x<7范围内的谷穗的概率.
如图,某 幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为6米,点E、D、B、C 在同一水平地面上.
幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为6米,点E、D、B、C 在同一水平地面上.
(1)改善后滑滑板会加长多少?(精确到0.01)
(2)若滑滑板的正前方留有4米长的空地 就能保证安全,已知原滑滑板的前方8米处的E
就能保证安全,已知原滑滑板的前方8米处的E
点有一棵大树,这样的改造是否可行?说明理由.(参考数据: ≈1.414,
≈1.414, ≈1.732,
≈1.732,
≈2.449.)

某超市推出两种优惠方法:①购1个水杯,赠送1包茶叶;②购水杯和茶叶一律按9折优惠.水杯每个定价20元,茶叶每包定价5元.小明需买4个水杯,茶叶若干包(不少于4包).
(1)分别写出两种优惠方法购买费用y(元)与所买茶叶包数x(包)之间的函数关系式;
(2)对 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小明需买这种水杯4个和茶叶12包,请你设计怎样购买最经济.
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度成直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?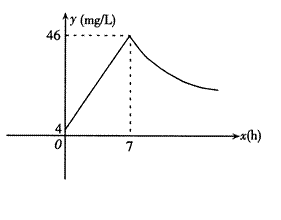

已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为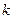 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
①当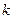 = 1时,是 ;
= 1时,是 ;
②当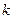 = 2时,是 ;
= 2时,是 ;
③当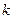 = 3时,是 .
= 3时,是 .
请证明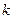 = 2时的结论.
= 2时的结论.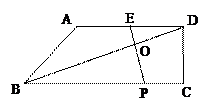

 的倒数是 【 】
的倒数是 【 】

 的值为 .
的值为 . 的坐标为
的坐标为 ,
, 为坐标原点,连结
为坐标原点,连结 ,将线段
,将线段 ,则点
,则点 的坐标为 .
的坐标为 .



 ,当
,当 时,再从-2<
时,再从-2< <2的范围内选取一个合适的整数
<2的范围内选取一个合适的整数 经过
经过 的三个点,已知
的三个点,已知 轴,点
轴,点 在
在 轴上,点
轴上,点 在
在 轴上,且
轴上,且 .
. 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式; 是抛物线对称轴上且在
是抛物线对称轴上且在 是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点
是等腰三角形?若存在,请在图中画出所有符合条件的P点,然后直接写出点

 粤公网安备 44130202000953号
粤公网安备 44130202000953号