已知的直径
,弦
与弦
交于点
.且
,垂足为点
.

(1)如图1,如果,求弦
的长;
(2)如图2,如果为弦
的中点,求
的余切值;
(3)联结、
、
,如果
是
的内接正
边形的一边,
是
的内接正
边形的一边,求
的面积.
设抛物线 (
( )与x轴的交点为A(
)与x轴的交点为A( , 0),B(
, 0),B( ,0),且
,0),且 ,其中
,其中 ,点P(a,b)为抛物线上一动点.
,点P(a,b)为抛物线上一动点.
(1)求抛物线的解析式;
(2)连接AC,过P点做直线PE∥AC交x轴于点E,交y轴于点E(O,t),当a取何值时t有最大值,最大值是多少?
(3)判断在(2)的条件中是否存在一点P,使以点A、C、P、E为顶点的四边形为平行四边形.若不存在试说明理由;若存在,试求出点P的坐标.
如图,已知 , 为 的两条直径,连接 , , 于点 ,点 是半径 的中点,连接 .
(1)设 的半径为1,若 ,求线段 的长.
(2)连接 , ,设 与 交于点 ,
①求证: .
②若 ,求 的度数.

(本题8分)已知锐角△ABC中,边BC长为12,高AD长为8
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K
①求 的值
的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
问题提出:
(1)如图1,已知,试确定一点
,使得以
,
,
,
为顶点的四边形为平行四边形,请画出这个平行四边形;
问题探究:
(2)如图2,在矩形中,
,
,若要在该矩形中作出一个面积最大的
,且使
,求满足条件的点
到点
的距离;
问题解决:
(3)如图3,有一座塔,按规定,要以塔
为对称中心,建一个面积尽可能大的形状为平行四边形的景区
.根据实际情况,要求顶点
是定点,点
到塔
的距离为50米,
,那么,是否可以建一个满足要求的面积最大的平行四边形景区
?若可以,求出满足要求的平行四边形
的最大面积;若不可以,请说明理由.(塔
的占地面积忽略不计)
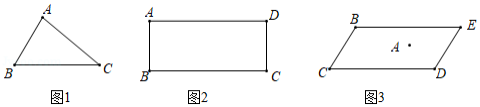
在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ 绕点A逆时针旋转,得到等腰Rt△
绕点A逆时针旋转,得到等腰Rt△ ,设旋转角为
,设旋转角为 ,记直线
,记直线 与
与 的交点为P.
的交点为P.

(1)如图1,当 时,线段
时,线段 的长等于 ,线段
的长等于 ,线段 的长等于 ;(直接填写结果)
的长等于 ;(直接填写结果)
(2)如图2,当 时,求证:
时,求证: ,且
,且 ;
;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)
如图,在 中, 是直径, 是弦, ,垂足为 ,过点 的 的切线与 延长线交于点 ,连接 .
(1)求证: 为 的切线;
(2)若 半径为3, ,求 .

问题提出
(1)如图①,在中,
,
,则
的外接圆半径
的值为 .
问题探究
(2)如图②,的半径为13,弦
,
是
的中点,
是
上一动点,求
的最大值.
问题解决
(3)如图③所示,、
、
是某新区的三条规划路,其中
,
,
,
所对的圆心角为
,新区管委会想在
路边建物资总站点
,在
,
路边分别建物资分站点
、
,也就是,分别在
、线段
和
上选取点
、
、
.由于总站工作人员每天都要将物资在各物资站点间按
的路径进行运输,因此,要在各物资站点之间规划道路
、
和
.为了快捷、环保和节约成本.要使得线段
、
、
之和最短,试求
的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
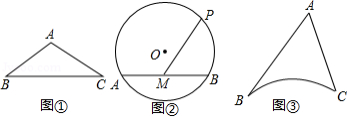
在 中, , 是边 上一动点,连接 ,将 绕点 逆时针旋转至 的位置,使得 .
(1)如图1,当 时,连接 ,交 于点 .若 平分 , ,求 的长;
(2)如图2,连接 ,取 的中点 ,连接 .猜想 与 存在的数量关系,并证明你的猜想;
(3)如图3,在(2)的条件下,连接 , .若 ,当 , 时,请直接写出 的值.

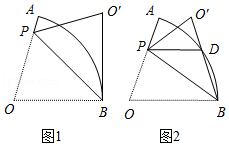
在扇形 中,半径 ,点 在 上,连结 ,将 沿 折叠得到△ .
(1)如图1,若 ,且 与 所在的圆相切于点 .
①求 的度数.
②求 的长.
(2)如图2, 与 相交于点 ,若点 为 的中点,且 ,求 的长.
如图, 是 的直径, , 是 的弦, 为 的中点, 与 交于点 ,过点 作 ,交 的延长线于点 ,且 平分 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 , ,求 的长.

如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
如图, 是半圆的直径, 为半圆的中点, , ,反比例函数 的图象经过点 ,则 的值为 .
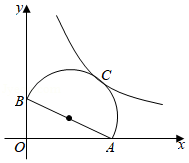
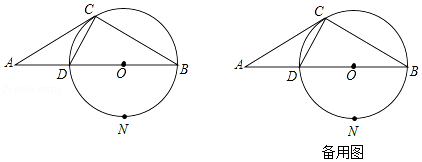
如图, 是 的内接三角形,点 在 上,点 在弦 上 不与 重合),且四边形 为菱形.
(1)求证: ;
(2)求证: ;
(3)已知 的半径为3.
①若 ,求 的长;
②当 为何值时, 的值最大?
