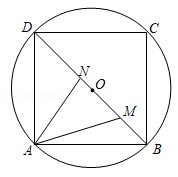
如图,正方形 内接于 ,线段 在对角线 上运动,若 的面积为 , ,则 周长的最小值是
| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为______________.
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.

(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.
在平面直角坐标系 O
O 中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒
中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
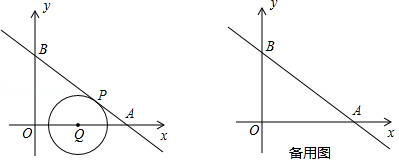
如图在平面直角坐标系中,直线 与 轴、 轴分别交于 、 两点,点 、 同时从点 出发,运动时间为 秒.其中点 沿射线 运动,速度为每秒4个单位长度,点 沿射线 运动,速度为每秒5个单位长度.以点 为圆心, 长为半径作 .
(1)求证:直线 是 的切线;
(2)过点 左侧 轴上的任意一点 ,作直线 的垂线 ,垂足为 .若 与 相切于点 ,求 与 的函数关系式(不需写出自变量的取值范围);
(3)在(2)的条件下,是否存在点 ,直线 、 、 轴与 同时相切?若存在,请直接写出此时点 的坐标;若不存在,请说明理由.
如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:①图形中全等的三角形只有三对;②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF= OA;⑤
OA;⑤ +
+
=2OP·OB.正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
如图,在△ABC中,AB=5,AC=9,S△ABC=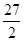 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.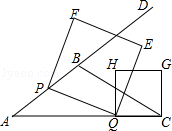
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
在 中, , 是边 上一动点,连接 ,将 绕点 逆时针旋转至 的位置,使得 .
(1)如图1,当 时,连接 ,交 于点 .若 平分 , ,求 的长;
(2)如图2,连接 ,取 的中点 ,连接 .猜想 与 存在的数量关系,并证明你的猜想;
(3)如图3,在(2)的条件下,连接 , .若 ,当 , 时,请直接写出 的值.

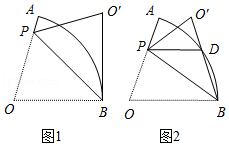
在扇形 中,半径 ,点 在 上,连结 ,将 沿 折叠得到△ .
(1)如图1,若 ,且 与 所在的圆相切于点 .
①求 的度数.
②求 的长.
(2)如图2, 与 相交于点 ,若点 为 的中点,且 ,求 的长.
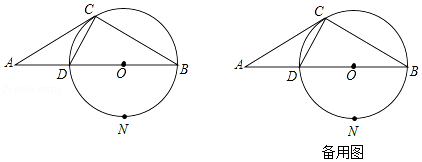
如图, 是 的直径, , 是 的弦, 为 的中点, 与 交于点 ,过点 作 ,交 的延长线于点 ,且 平分 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 , ,求 的长.

如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
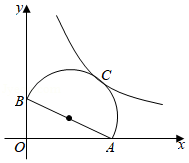
如图, 是半圆的直径, 为半圆的中点, , ,反比例函数 的图象经过点 ,则 的值为 .
如图, 是 的内接三角形,点 在 上,点 在弦 上 不与 重合),且四边形 为菱形.
(1)求证: ;
(2)求证: ;
(3)已知 的半径为3.
①若 ,求 的长;
②当 为何值时, 的值最大?

在平面直角坐标系 中,点 的坐标为 , ,点 的坐标为 , ,且 , ,若 , 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点 , 的"相关矩形",如图为点 , 的"相关矩形"示意图.
(1)已知点 的坐标为 ,
①若点 的坐标为 ,求点 , 的"相关矩形"的面积;
②点 在直线 上,若点 , 的"相关矩形"为正方形,求直线 的表达式;
(2) 的半径为 ,点 的坐标为 ,若在 上存在一点 ,使得点 , 的"相关矩形"为正方形,求 的取值范围.
