(本小题满分5分)已知菱形纸片ABCD的边长为 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点 处,
处, 与
与 H分别交
H分别交 与
与 于点M、N.若点
于点M、N.若点 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.


 |
|||
 |
图1 图2 备用图
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形 的面积;
的面积;
(2)实验探究:设AE的长为 ,若重叠四边形
,若重叠四边形 存在.试用含
存在.试用含 的代数式表示重叠四边形
的代数式表示重叠四边形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
如图,正方形ABCD,E为AB上的动点,(E不与A、B重合)联结DE,作DE的中垂线,交AD于点F.
(1)若E为AB中点,则 .
.
(2)若E为AB的 等分点(靠近点A),
等分点(靠近点A),
则 .
.
如图,把直角梯形 沿
沿 方向平移得到梯形
方向平移得到梯形 ,
, 与
与 相交于点
相交于点 ,
, =20cm,
=20cm, =5cm,
=5cm, =4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
=4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
如图9,边长为5的正方形 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)( )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
的坐标;若不存在,说明理由.
某过街天桥的截面图为梯形,如图7所示,其中天桥斜面 的坡度为
的坡度为
( 是指铅直高度
是指铅直高度 与水平宽度
与水平宽度 的比),
的比), 的长为10m,天桥另一斜面
的长为10m,天桥另一斜面
坡角 =
= .
.
(1)写出过街天桥斜面 的坡度;
的坡度;
(2)求 的长;
的长;
(3)若决定对该过街天桥进行改建,使 斜面的坡度变缓,将其
斜面的坡度变缓,将其 坡角改为
坡角改为 ,
,
方便群众,改建后斜面为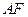 .试计算此改建需占路面的宽度
.试计算此改建需占路面的宽度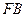 的长(结果精确0.01)
的长(结果精确0.01)
如图5,在平行四边形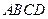 中,
中,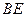 平分
平分 交
交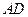 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
.
求证:(1) ;
;
(2)若 ,则判断四边形
,则判断四边形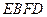 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.
如图3,四边形 为菱形,点
为菱形,点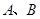 在以点
在以点 为圆心的
为圆心的 上,
上,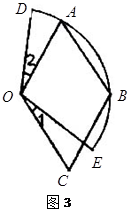
若 则扇形
则扇形 的面积为
的面积为
A. |
B.2 |
C. |
D.3 |