初中数学矩形的性质填空题

如图，矩形中，，，为中点，为上一点，将沿折叠后，点恰好落到上的点处，则折痕的长是　　．

如图，在矩形中，，，为边上一点，将沿折叠，使得落到矩形内点的位置，连接，若，则　　．

如图，在平面直角坐标系中，矩形的顶点落在坐标原点，点、点分别位于轴，轴的正半轴，为线段上一点，将沿翻折，点恰好落在对角线上的点处，反比例函数经过点．二次函数的图象经过、、三点，则该二次函数的解析式为　　．（填一般式）

如图，矩形硬纸片的顶点在轴的正半轴及原点上滑动，顶点在轴的正半轴及原点上滑动，点为的中点，，．给出下列结论：①点从点出发，到点运动至点为止，点经过的路径长为；②的面积最大值为144；③当最大时，点的坐标为，．其中正确的结论是　　．（填写序号）

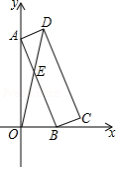
如图，反比例函数的图象经过矩形对角线的交点，分别交，于点、．若四边形的面积为12，则的值为　　．

矩形中，为边上一点，将矩形沿翻折后，点的对应点为，延长交于点，若，则的大小为　　度．

矩形中，为边上一点，将矩形沿翻折后，点的对应点为，延长交于点，若，则的大小为　　度．

如图，矩形的两边分别与坐标轴平行，顶点，都在双曲线（常数，上，若顶点的坐标为，则直线的函数表达式是　　．

如图，把某矩形纸片沿，折叠（点，在边上，点，在边上），使点和点落在边上同一点处，点的对称点为点，点的对称点为点，若，△的面积为4，△的面积为1，则矩形的面积等于　　．

如图，四边形是矩形，，，以点为圆心，长为半径画弧，交于点，交的延长线于点，则图中阴影部分的面积是　　．

如图，在矩形中，，，以点为圆心，长为半径画弧，交于点，图中阴影部分的面积是　　（结果保留．

如图，把一张长为4，宽为2的矩形纸片，沿对角线折叠，则重叠部分的面积为　　．

已知任一平面封闭图形，现在其外部存在一水平放置的矩形，使得矩形每条边都与该图形有至少一个交点，且构成该图形的所有点都在矩形内部或矩形边上，那么就称这个矩形为“该图形的矩形”，且这个矩形的水平长成为该图形的宽，铅直高称为该图形的高．如图，边长为1的菱形的一条边水平放置，已知“该菱形的矩形”的“高”是“宽”的，则该“菱形的矩形”的“宽”为　　．

如图，矩形中，，将矩形绕点顺时针旋转，点、分别落在点、处．如果点、、在同一条直线上，那么的值为　　．

如图，是矩形的对称中心，，，若一个反比例函数的图象经过点，交于点，则点的坐标为　　．