如图1, 为矩形 的边 上一点,点 从点 出发沿折线 运动到点 停止,点 从点 出发沿 运动到点 停止,它们运动的速度都是 .若点 、点 同时开始运动,设运动时间为 , 的面积为 ,已知 与 之间的函数图象如图2所示.
给出下列结论:①当 时, 是等腰三角形;② ;③当 时, ;④在运动过程中,使得 是等腰三角形的 点一共有3个;⑤ 与 相似时, .
其中正确结论的序号是 .

如图,在矩形 中,
中, 为坐标原点,
为坐标原点, 、
、 分别在
分别在 轴、
轴、 轴上,点
轴上,点 的坐标为
的坐标为 ,
, ,
, ,将
,将 沿
沿 所在直线对折后,点
所在直线对折后,点 落在点
落在点 处,则点
处,则点 的坐标为
的坐标为


A. ,
, B.
B. C.
C. ,
, D.
D. ,
,
如图,矩形 的对角线 与 交于点 ,过点 作 的垂线分别交 , 于 , 两点.若 , ,则 的长度为

A.1B.2C. D.
如图,将矩形 沿 折叠,使点 落在 边上的点 处,过点 作 交 于点 ,连接 .
(1)求证:四边形 是菱形;
(2)探究线段 、 、 之间的数量关系,并说明理由;
(3)若 , ,求 的长.

如图,矩形 中, , ,点 从点 出发,以 的速度沿 方向匀速运动,同时点 从点 出发,以 的速度沿 方向匀速运动,当一个点到达点 时,另一个点也随之停止.设运动时间为 , 的面积为 ,下列能大致反映 与 之间函数关系的图象是

A.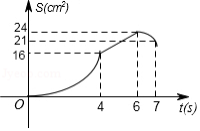
B.
C.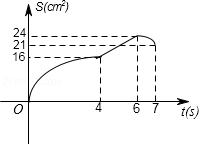
D.
矩形 与 如图放置,点 , , 共线,点 , , 共线,连接 ,取 的中点 ,连接 .若 , ,则

A.1B. C. D.
在矩形 中, , 是边 上一点,把 沿直线 折叠,顶点 的对应点是点 ,过点 作 ,垂足为 且在 上, 交 于点 .
(1)如图1,若点 是 的中点,求证: ;
(2)如图2,①求证: ;
②当 ,且 时,求 的值;
③当 时,求 的值.

如图,将面积为 的矩形 沿对角线 折叠,点 的对应点为点 ,连接 交 于点 .若 ,则 的长为 .

如图,在平面直角坐标系中,矩形 的顶点 的坐标为 ,直线 与边 , 分别相交于点 , ,函数 的图象过点 .
(1)试说明点 也在函数 的图象上;
(2)将直线 沿 轴的负方向平移得到直线 ,当直线 与函数 的图象仅有一个交点时,求直线 的解析式.

如图,对折矩形纸片 ,使 与 重合,得到折痕 ,将纸片展平;再一次折叠,使点 落到 上的点 处,折痕 交 于 ;延长 交 于 .求证:
(1) ;
(2) 为等边三角形.

如图,直线 、 垂直相交于点 ,曲线 关于点 成中心对称,点 的对称点是点 , 于点 , 于点 .若 , ,则阴影部分的面积之和为 .

如图,点 是矩形纸片 的对称中心, 是 上一点,将纸片沿 折叠后,点 恰好与点 重合.若 ,则折痕 的长为 .
