如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
如图,在 中, , 、 分别是边 、 的中点,过点 作 交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若四边形 的面积为24, ,求 的长.

如图,在 中, , ,垂足分别为 , ,且 .
(1)求证: 是菱形;
(2)若 , ,求 的面积.

如图,四边形 中, , 相交于点 , 是 的中点, , , .
(1)求证:四边形 是平行四边形;
(2)若 ,求 的面积.

如图,四边形 是轴对称图形,且直线 是对称轴, ,则下列结论: ① ; ② ; ③ 四边形 是菱形; ④ .其中正确的是 (只填写序号)

如图,在 中,用直尺和圆规作 的平分线 交 于点 .若 , ,则 的长为

A.5B.6C.8D.12
如图,在 中,以点 为圆心, 长为半径画弧交 于点 ,再分别以点 、 为圆心,大于 的相同长为半径画弧,两弧交于点 ;连接 并延长交 于点 ,连接 ,则所得四边形 是菱形.
(1)根据以上尺规作图的过程,求证:四边形 是菱形;
(2)若菱形 的周长为16, ,求 的大小.

如图,将等边 绕点 顺时针旋转 得到 ,连接 , .则下列结论:
① ;② ;③四边形 是菱形.
其中正确的个数是
A.0B.1C.2D.3
我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
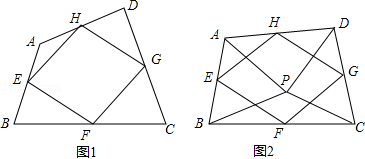
(1)如图1,四边形 中,点 , , , 分别为边 , , , 的中点.求证:中点四边形 是平行四边形;
(2)如图2,点 是四边形 内一点,且满足 , , ,点 , , , 分别为边 , , , 的中点,猜想中点四边形 的形状,并证明你的猜想;
(3)若改变(2)中的条件,使 ,其他条件不变,直接写出中点四边形 的形状.(不必证明)
如图, 是 的角平分线,它的垂直平分线分别交 , , 于点 , , ,连接 , .
(1)请判断四边形 的形状,并说明理由;
(2)若 , , ,点 是 上的一个动点,求 的最小值.

如图,在矩形 中, 是 上一点, 垂直平分 ,分别交 、 、 于点 、 、 ,连接 、 .
(1)求证:四边形 是菱形;
(2)若 , 为 的中点, ,求 的长.
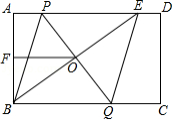
如图,四边形 是平行四边形,以点 为圆心、 的长为半径画弧交 于点 ,再分别以点 , 为圆心、大于 的长为半径画弧,两弧交于点 ,作射线 交 于点 ,连接 .下列结论中不一定成立的是

A. B. C. 平分 D.
如图,在四边形 中, , , 平分 .
(1)求证:四边形 是菱形;
(2)过点 作 ,交 的延长线于点 ,若 , ,求四边形 的周长.

如图,在 中, , , , 分别为 、 、 的中点,则下列结论:① ,②四边形 为菱形,③ .其中正确的结论是 .(填写所有正确结论的序号)
