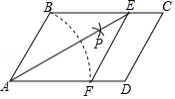
如图,在 中,以点 为圆心, 长为半径画弧交 于点 ,再分别以点 、 为圆心,大于 的相同长为半径画弧,两弧交于点 ;连接 并延长交 于点 ,连接 ,则所得四边形 是菱形.
(1)根据以上尺规作图的过程,求证:四边形 是菱形;
(2)若菱形 的周长为16, ,求 的大小.
推荐套卷
如图,在 中,以点 为圆心, 长为半径画弧交 于点 ,再分别以点 、 为圆心,大于 的相同长为半径画弧,两弧交于点 ;连接 并延长交 于点 ,连接 ,则所得四边形 是菱形.
(1)根据以上尺规作图的过程,求证:四边形 是菱形;
(2)若菱形 的周长为16, ,求 的大小.
