初中数学菱形的判定与性质试题

如图，在平行四边形 ABCD中，点 E， F， G， H分别在边 AB， BC， CD， DA上， AE＝ CG， AH＝ CF，且 EG平分∠ HEF．

（1）求证：四边形 EFGH是菱形；

（2）若 EF＝4，∠ HEF＝60°，求 EG的长．

如图，在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE＝CG，AH＝CF，且EG平分∠HEF．

（1）求证：四边形EFGH是菱形；

（2）若EF＝4，∠HEF＝60°，求EG的长．

如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（　　）

A．45°B．50°C．60°D．75°

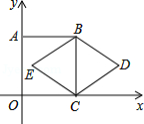
如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点D的坐标是　　．

如图，在四边形中，是钝角，，平分，若， $\mathit{BD}=2\sqrt{6},\mathrm{}\sin \angle \mathit{DBC}=\frac{\sqrt{3}}{3}$，求对角线的长．

如图，在四边形中，，，点在边上．

（1）判断四边形的形状并加以证明；

（2）若，以过点的直线为轴，将四边形折叠，使点、分别落在点、上，且经过点，折痕与四边形的另一交点为．

①在图2中作出四边形（保留作图痕迹，不必说明作法和理由）；

②如果，那么 $\frac{\mathit{AP}}{\mathit{PB}}$为何值时，．

如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．

（1）求证：四边形AECF是菱形；

（2）若AB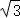＝，∠DCF＝30°，求四边形AECF的面积．（结果保留根号）

如图，矩形 的对角线 ， 相交于点 ， 关于 的对称图形为 ．

（1）求证：四边形 是菱形；

（2）连接 ，若 ， ．

①求 的值；

②若点 为线段 上一动点（不与点 重合），连接 ，一动点 从点 出发，以 的速度沿线段 匀速运动到点 ，再以 的速度沿线段 匀速运动到点 ，到达点 后停止运动，当点 沿上述路线运动到点 所需要的时间最短时，求 的长和点 走完全程所需的时间．

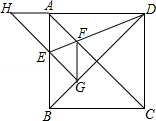
如图，正方形 ABCD的边长为1， AC， BD是对角线．将△ DCB绕着点 D顺时针旋转45°得到△ DGH， HG交 AB于点 E，连接 DE交 AC于点 F，连接 FG．则下列结论：

①四边形 AEGF是菱形

②△ AED≌△ GED

③∠ DFG＝112.5°

④ BC+ FG＝1.5

其中正确的结论是 　　．

如图①，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\angle \mathit{BAC}=120°$，点 $E$是边 $\mathit{AB}$的中点，点 $P$是边 $\mathit{BC}$上一动点，设 $\mathit{PC}=x$， $\mathit{PA}+\mathit{PE}=y$．图②是 $y$关于 $x$的函数图象，其中 $H$是图象上的最低点．那么 $a+b$的值为　　．

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{BD}$ ， $\mathit{CE}$ 分别是边 $\mathit{AC}$ ， $\mathit{AB}$ 上的中线， $\mathit{BD}\perp \mathit{CE}$ 于点 $O$ ，点 $M$ ， $N$ 分别 $\mathit{OB}$ ， $\mathit{OC}$ 的中点，若 $\mathit{OB}=8$ ， $\mathit{OC}=6$ ，则四边形 $\mathit{DEMN}$ 的周长是 $($ 　　 $)$

A．

14

B．

20

C．

22

D．

28

如图， $\mathit{AB}$ 是 $\odot O$ 的直径，弦 $\mathit{CD}\perp \mathit{AB}$ ，垂足为 $E$ ， $\angle \mathit{BCD}=30°$ ， $\mathit{CD}=2\sqrt{3}$ ，则阴影部分面积 $S_{\mathit{阴影}}=$ 　　．

如图， $▱\mathit{ABCD}$ 的对角线 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ，以 $\mathit{AB}$ 为直径的 $\odot O$ 经过点 $E$ ，与 $\mathit{AD}$ 交于点 $F$ ， $G$ 是 $\mathit{AD}$ 延长线上一点，连接 $\mathit{BG}$ ，交 $\mathit{AC}$ 于点 $H$ ，且 $\angle \mathit{DBG}=\frac{1}{2}\angle \mathit{BAD}$ ．

（1）求证： $\mathit{BG}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{CH}=3$ ， $\tan \angle \mathit{DBG}=\frac{1}{2}$ ，求 $\odot O$ 的直径．

如图，二次函数 $y=x^2+\mathit{bx}+c$ 的图象交 $x$ 轴于点 $A(-3,0)$ ， $B(1,0)$ ，交 $y$ 轴于点 $C$ ．点 $P(m,0)$ 是 $x$ 轴上的一动点， $\mathit{PM}\perp x$ 轴，交直线 $\mathit{AC}$ 于点 $M$ ，交抛物线于点 $N$ ．

（1）求这个二次函数的表达式；

（2）①若点 $P$ 仅在线段 $\mathit{AO}$ 上运动，如图，求线段 $\mathit{MN}$ 的最大值；

②若点 $P$ 在 $x$ 轴上运动，则在 $y$ 轴上是否存在点 $Q$ ，使以 $M$ ， $N$ ， $C$ ， $Q$ 为顶点的四边形为菱形．若存在，请直接写出所有满足条件的点 $Q$ 的坐标；若不存在，请说明理由．

能够完全重合的平行四边形纸片 $\mathit{ABCD}$ 和 $\mathit{AEFG}$ 按图①方式摆放，其中 $\mathit{AD}=\mathit{AG}=5$ ， $\mathit{AB}=9$ ．点 $D$ ， $G$ 分别在边 $\mathit{AE}$ ， $\mathit{AB}$ 上， $\mathit{CD}$ 与 $\mathit{FG}$ 相交于点 $H$ ．

【探究】求证：四边形 $\mathit{AGHD}$ 是菱形．

【操作一】固定图①中的平行四边形纸片 $\mathit{ABCD}$ ，将平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 顺时针旋转一定的角度，使点 $F$ 与点 $C$ 重合，如图②．则这两张平行四边形纸片未重叠部分图形的周长和为 　    　．

【操作二】将图②中的平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 继续顺时针旋转一定的角度，使点 $E$ 与点 $B$ 重合，连接 $\mathit{DG}$ ， $\mathit{CF}$ ，如图③，若 $\sin \angle \mathit{BAD}=\frac{4}{5}$ ，则四边形 $\mathit{DCFG}$ 的面积为 　　．