如图,正方形 ABCD的边长为1, AC, BD是对角线.将△ DCB绕着点 D顺时针旋转45°得到△ DGH, HG交 AB于点 E,连接 DE交 AC于点 F,连接 FG.则下列结论:
①四边形 AEGF是菱形
②△ AED≌△ GED
③∠ DFG=112.5°
④ BC+ FG=1.5
其中正确的结论是 .
如图,四边形 是轴对称图形,且直线 是对称轴, ,则下列结论: ① ; ② ; ③ 四边形 是菱形; ④ .其中正确的是 (只填写序号)

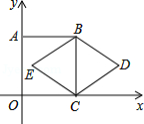
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .
如图,先有一张矩形纸片,
,
,点
,
分别在矩形的边
,
上,将矩形纸片沿直线
折叠,使点
落在矩形的边
上,记为点
,点
落在
处,连接
,交
于点
,连接
.下列结论:
①;
②四边形是菱形;
③,
重合时,
;
④的面积
的取值范围是
.
其中正确的是 (把正确结论的序号都填上).

如图, 、 、 是 上的三点,且四边形 是菱形.若点 是圆上异于 、 、 的另一点,则 的度数是 .

如图①,在 中, , ,点 是边 的中点,点 是边 上一动点,设 , .图②是 关于 的函数图象,其中 是图象上的最低点.那么 的值为 .

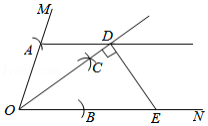
如图,已知是一个锐角,以点
为圆心,任意长为半径画弧,分别交
、
于点
、
,再分别以点
、
为圆心,大于
长为半径画弧,两弧交于点
,画射线
.过点
作
,交射线
于点
,过点
作
,交
于点
.设
,
,则
.
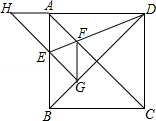
如图,在 中, , , , 分别为 、 、 的中点,则下列结论:① ,②四边形 为菱形,③ .其中正确的结论是 .(填写所有正确结论的序号)

如图,在等边三角形中,
,点
为边
的中点,点
为边
上的任意一点(不与点
,
重合),若点
关于直线
的对称点
恰好落在等边三角形
的边上,则
的长为
.
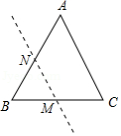
如图,在四边形 中, , 且 , .给出以下判断:
① 垂直平分 ;
②四边形 的面积 ;
③顺次连接四边形 的四边中点得到的四边形可能是正方形;
④当 , , , 四点在同一个圆上时,该圆的半径为 ;
⑤将 沿直线 对折,点 落在点 处,连接 并延长交 于点 ,当 时,点 到直线 的距离为 .
其中正确的是 .(写出所有正确判断的序号)
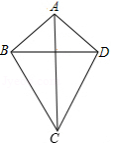
规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若、
的坐标分别为
,
,
是二次函数
的图象上在第一象限内的任意一点,
垂直直线
于点
,则四边形
是广义菱形.其中正确的是 .(填序号)
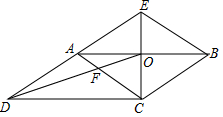
如图, CE是▱ ABCD的边 AB的垂直平分线,垂足为点 O, CE与 DA的延长线交于点 E.连接 AC, BE, DO, DO与 AC交于点 F,则下列结论:
①四边形 ACBE是菱形;
②∠ ACD=∠ BAE;
③ AF: BE=2:3;
④ S 四边形 AFOE: S △ COD=2:3.
其中正确的结论有 .(填写所有正确结论的序号)