初中数学菱形的判定与性质解答题

如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

（1）求证：△BDF是等腰三角形；

（2）如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．

①判断四边形BFDG的形状，并说明理由；

②若AB＝6，AD＝8，求FG的长．

已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△ CFE中， CF＝6， CE＝12，∠ FCE＝45°，以点 C为圆心，以任意长为半径作 $\stackrel{⏜}{\mathit{AD}}$ ，再分别以点 A和点 D为圆心，大于 $\frac{1}{2}$ AD长为半径作弧，交 EF于点 B， AB∥ CD．

（1）求证：四边形 ACDB为△ FEC的亲密菱形；

（2）求四边形 ACDB的面积．

如图，在平行四边形 ABCD中， E， F分别是 AB， BC边上的中点， CE⊥ AB，垂足为 E， AF⊥ BC，垂足为 F， AF与 CE相交于点 G；

（1）求证：△ CFG≌△ AEG；

（2）若 AB＝6，求四边形 AGCD的对角线 GD的长．

邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第 n次操作余下的四边形是菱形，则称原平行四边形为 n阶准菱形，如图1，▱ ABCD中，若 AB＝1， BC＝2，则▱ ABCD为1阶准菱形．

（1）猜想与计算：

邻边长分别为3和5的平行四边形是 　　阶准菱形；已知▱ ABCD的邻边长分别为 a， b（ a＞ b），满足 a＝8 b+ r， b＝5 r，请写出▱ ABCD是 　　阶准菱形．

（2）操作与推理：

小明为了剪去一个菱形，进行了如下操作：如图2，把▱ ABCD沿 BE折叠（点 E在 AD上），使点 A落在 BC边上的点 F处，得到四边形 ABFE．请证明四边形 ABFE是菱形．

如图，四边形 ABCD中， MA＝ MC， MB＝ MD，以 AB为直径的圆 O过点 M且与 DC延长线相切于点 E．

（1）求证：四边形 ABCD是菱形；

（2）若 AB＝4，求 $\stackrel{⏜}{\mathit{BM}}$ 的长（结果请保留π）

如图，在△ ABC中，∠ C＝90°，∠ B＝30°， AD是△ ABC的角平分线， DE∥ BA交 AC于点 E， DF∥ CA交 AB于点 F，已知 CD＝3．

（1）求 AD的长；

（2）求四边形 AEDF的周长．（注意：本题中的计算过程和结果均保留根号）

如图，在平行四边形 ABCD中，点 E， F， G， H分别在边 AB， BC， CD， DA上， AE＝ CG， AH＝ CF，且 EG平分∠ HEF．

（1）求证：四边形 EFGH是菱形；

（2）若 EF＝4，∠ HEF＝60°，求 EG的长．

如图，在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE＝CG，AH＝CF，且EG平分∠HEF．

（1）求证：四边形EFGH是菱形；

（2）若EF＝4，∠HEF＝60°，求EG的长．

如图，在四边形中，是钝角，，平分，若， $\mathit{BD}=2\sqrt{6},\mathrm{}\sin \angle \mathit{DBC}=\frac{\sqrt{3}}{3}$，求对角线的长．

如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．

（1）求证：四边形AECF是菱形；

（2）若AB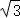＝，∠DCF＝30°，求四边形AECF的面积．（结果保留根号）

如图，矩形 的对角线 ， 相交于点 ， 关于 的对称图形为 ．

（1）求证：四边形 是菱形；

（2）连接 ，若 ， ．

①求 的值；

②若点 为线段 上一动点（不与点 重合），连接 ，一动点 从点 出发，以 的速度沿线段 匀速运动到点 ，再以 的速度沿线段 匀速运动到点 ，到达点 后停止运动，当点 沿上述路线运动到点 所需要的时间最短时，求 的长和点 走完全程所需的时间．

如图， $▱\mathit{ABCD}$ 的对角线 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ，以 $\mathit{AB}$ 为直径的 $\odot O$ 经过点 $E$ ，与 $\mathit{AD}$ 交于点 $F$ ， $G$ 是 $\mathit{AD}$ 延长线上一点，连接 $\mathit{BG}$ ，交 $\mathit{AC}$ 于点 $H$ ，且 $\angle \mathit{DBG}=\frac{1}{2}\angle \mathit{BAD}$ ．

（1）求证： $\mathit{BG}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{CH}=3$ ， $\tan \angle \mathit{DBG}=\frac{1}{2}$ ，求 $\odot O$ 的直径．

能够完全重合的平行四边形纸片 $\mathit{ABCD}$ 和 $\mathit{AEFG}$ 按图①方式摆放，其中 $\mathit{AD}=\mathit{AG}=5$ ， $\mathit{AB}=9$ ．点 $D$ ， $G$ 分别在边 $\mathit{AE}$ ， $\mathit{AB}$ 上， $\mathit{CD}$ 与 $\mathit{FG}$ 相交于点 $H$ ．

【探究】求证：四边形 $\mathit{AGHD}$ 是菱形．

【操作一】固定图①中的平行四边形纸片 $\mathit{ABCD}$ ，将平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 顺时针旋转一定的角度，使点 $F$ 与点 $C$ 重合，如图②．则这两张平行四边形纸片未重叠部分图形的周长和为 　    　．

【操作二】将图②中的平行四边形纸片 $\mathit{AEFG}$ 绕着点 $A$ 继续顺时针旋转一定的角度，使点 $E$ 与点 $B$ 重合，连接 $\mathit{DG}$ ， $\mathit{CF}$ ，如图③，若 $\sin \angle \mathit{BAD}=\frac{4}{5}$ ，则四边形 $\mathit{DCFG}$ 的面积为 　　．

如图，在四边形中，，对角线的垂直平分线与边、分别相交于点、．

（1）求证：四边形是菱形；

（2）若，，求菱形的周长．

如图，在菱形 $\mathit{ABCD}$ 中，将对角线 $\mathit{AC}$ 分别向两端延长到点 $E$ 和 $F$ ，使得 $\mathit{AE}=\mathit{CF}$ ．连接 $\mathit{DE}$ ， $\mathit{DF}$ ， $\mathit{BE}$ ， $\mathit{BF}$ ．

求证：四边形 $\mathit{BEDF}$ 是菱形．