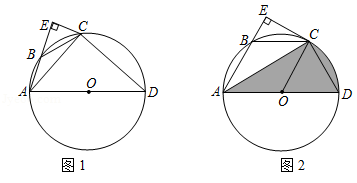
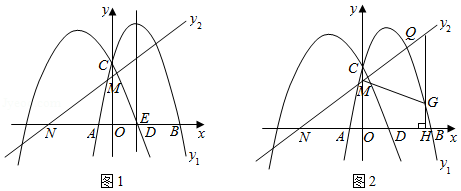如图1,四边形 内接于 , 为直径,点 作 于点 ,连接 .
(1)求证: ;
(2)若 是 的切线, ,连接 ,如图2.
①请判断四边形 的形状,并说明理由;
②当 时,求 , 与 围成阴影部分的面积.
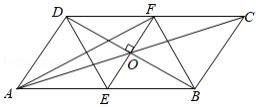
如图,在四边形 中,对角线 与 交于点 ,已知 , ,过点 作 ,分别交 、 于点 , ,连接 , .
(1)求证:四边形 是菱形:
(2)设 , , ,求 的长.
如图,在平面直角坐标系中,正方形 的两直角边分别在坐标轴的正半轴上,分别过 , 的中点 , 作 , 的平行线,相交于点 ,已知 .
(1)求证:四边形 为菱形.
(2)求四边形 的面积.
(3)若点 在 轴正半轴上(异于点 ,点 在 轴上,平面内是否存在点 ,使得以点 , , , 为顶点的四边形与四边形 相似?若存在,求点 的坐标;若不存在,试说明理由.

如图,在四边形 中,
中, ,
, ,点
,点 在边
在边 上.
上.
(1)判断四边形 的形状并加以证明;
的形状并加以证明;
(2)若 ,以过点
,以过点 的直线为轴,将四边形
的直线为轴,将四边形 折叠,使点
折叠,使点 、
、 分别落在点
分别落在点 、
、 上,且
上,且 经过点
经过点 ,折痕与四边形的另一交点为
,折痕与四边形的另一交点为 .
.
①在图2中作出四边形 (保留作图痕迹,不必说明作法和理由);
(保留作图痕迹,不必说明作法和理由);
②如果 ,那么
为何值时,
,那么
为何值时, .
.

如图,二次函数 的图象交 轴于点 , ,交 轴于点 .点 是 轴上的一动点, 轴,交直线 于点 ,交抛物线于点 .
(1)求这个二次函数的表达式;
(2)①若点 仅在线段 上运动,如图,求线段 的最大值;
②若点 在 轴上运动,则在 轴上是否存在点 ,使以 , , , 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点 的坐标;若不存在,请说明理由.

某校开展了一次综合实践活动,参加该活动的每个学生持有两张宽为 ,长足够的矩形纸条.探究两张纸条叠放在一起,重叠部分的形状和面积.
如图1所示,一张纸条水平放置不动,另一张纸条与它成 的角,将该纸条从右往左平移.
(1)写出在平移过程中,重叠部分可能出现的形状.
(2)当重叠部分的形状为如图2所示的四边形 时,求证:四边形 是菱形.
(3)设平移的距离为 ,两张纸条重叠部分的面积为 .求 与 的函数关系式,并求 的最大值.

如图1,抛物线与抛物线
相交
轴于点
,抛物线
与
轴交于
、
两点(点
在点
的右侧),直线
交
轴负半轴于点
,交
轴于点
,且
.
(1)求抛物线的解析式与
的值;
(2)抛物线的对称轴交
轴于点
,连接
,在
轴上方的对称轴上找一点
,使以点
,
,
为顶点的三角形与
相似,求出
的长;
(3)如图2,过抛物线上的动点
作
轴于点
,交直线
于点
,若点
是点
关于直线
的对称点,是否存在点
(不与点
重合),使点
落在
轴上?若存在,请直接写出点
的横坐标,若不存在,请说明理由.