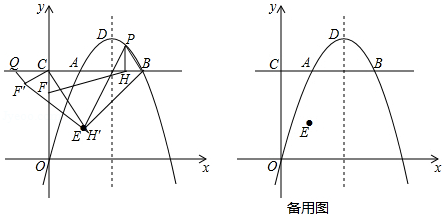
如图，在平面直角坐标系中，点在抛物线上，且横坐标为1，点与点关于抛物线的对称轴对称，直线与轴交于点，点为抛物线的顶点，点的坐标为．
（1）求线段的长；
（2）点为线段上方抛物线上的任意一点，过点作的垂线交于点，点为轴上一点，当的面积最大时，求的最小值；
（3）在（2）中，取得最小值时，将绕点顺时针旋转后得到△，过点作的垂线与直线交于点，点为抛物线对称轴上的一点，在平面直角坐标系中是否存在点，使以点，，，为顶点的四边形为菱形，若存在，请直接写出点的坐标，若不存在，请说明理由．
（1）如图，已知∠BAC+∠ACD=180°，AE平分∠BAC，CF平分∠ACG.则∠1与∠2的关系怎样？试证明你的结论．(要求写出推理过程和每一步的理由)
（2）若将（1）中的条件改为∠BAC=∠ACG，其它条件不变，则∠1与∠2的上述关系还成立吗？（直接写出结论即可）
某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年的月均用水量（单位：吨），并将调查数据进行了如下整理：
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
列频数分布表：
| 分组 |
划记 |
频数 |
| 2.0<x≤3．5 |
正正一 |
11 |
| 3.5<x≤5．0 |
正正正止 |
19 |
| 5.0<x≤6．5 |
||
| 6.5<x≤8．0 |
||
| 8.0<x≤9．5 |
ㄒ |
2 |
| 合计 |
 |
50 |
画频数分布直方图：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）从直方图中你能得到什么信息？（写出两条即可）
（3）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1．5倍价格收费．若要使60%的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？
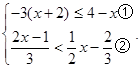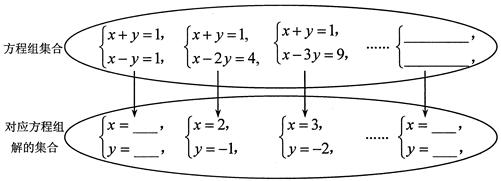
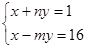并求它的所有整数解．下图是按一定规律排列的方程组集合和它解的集合的对应关系图，若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、……方程组n．
（1）将方程组1的解填入图中；
（2）请依据方程组和它的解变化的规律，将方程组n和它的解直接填入集合图中；
（3）若方程组
的解是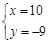
，求m、n的值，并判断该方程组是否符合（2）中的规律？
；
，试求方程中的
值．
粤公网安备 44130202000953号