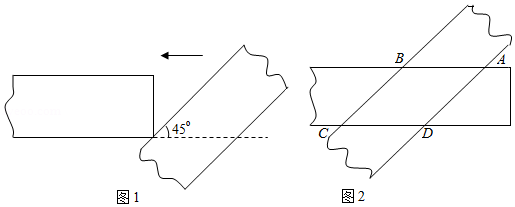
某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为

更新 2022-09-04
科目数学
题型解答题
难度较难
浏览 190

挑错有奖

某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为 $6 cm$ ，长足够的矩形纸条．探究两张纸条叠放在一起，重叠部分的形状和面积．

如图1所示，一张纸条水平放置不动，另一张纸条与它成 $45 °$ 的角，将该纸条从右往左平移．

（1）写出在平移过程中，重叠部分可能出现的形状．

（2）当重叠部分的形状为如图2所示的四边形 $ABCD$ 时，求证：四边形 $ABCD$ 是菱形．

（3）设平移的距离为 $xcm (0 < x ⩽ 6 + 6 \sqrt{2})$ ，两张纸条重叠部分的面积为 $sc m^{2}$ ．求 $s$ 与 $x$ 的函数关系式，并求 $s$ 的最大值．

登录免费查看答案和解析

相关试题

如图，点 $E$ 是 $ΔABC$ 的内心， $AE$ 的延长线和 $ΔABC$ 的外接圆 $⊙ O$ 相交于点 $D$ ，过 $D$ 作直线 $DG / / BC$ ．

（1）求证： $DG$ 是 $⊙ O$ 的切线；

（2）若 $DE = 6$ ， $BC = 6 \sqrt{3}$ ，求优弧 $\hat{BAC}$ 的长．

题型：未知
难度：未知

收藏答案/解析

如图，已知一次函数 $y_{1} = kx + b$ 与反比例函数 $y_{2} = \frac{m}{x}$ 的图象在第一、第三象限分别交于 $A (3, 4)$ ， $B (a, - 2)$ 两点，直线 $AB$ 与 $y$ 轴， $x$ 轴分别交于 $C$ ， $D$ 两点．

（1）求一次函数和反比例函数的解析式；

（2）比较大小： $AD$ 　　 $BC$ （填“ $>$ ”或“ $<$ ”或“ $=$ ” $)$ ；

（3）直接写出 $y_{1} < y_{2}$ 时 $x$ 的取值范围．

题型：未知
难度：未知

收藏答案/解析

襄阳卧龙大桥横跨汉江，是我市标志性建筑之一．某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分（上塔柱 $BC$ 和塔冠 $BE)$ 进行了测量．如图所示，最外端的拉索 $AB$ 的底端 $A$ 到塔柱底端 $C$ 的距离为 $121 m$ ，拉索 $AB$ 与桥面 $AC$ 的夹角为 $37 °$ ，从点 $A$ 出发沿 $AC$ 方向前进 $23.5 m$ ，在 $D$ 处测得塔冠顶端 $E$ 的仰角为 $45 °$ ．请你求出塔冠 $BE$ 的高度（结果精确到 $0.1 m$ ．参考数据 $\sin 37 ° \approx 0.60$ ， $\cos 37 ° \approx 0.80$ ， $\tan 37 ° \approx 0.75$ ， $\sqrt{2} \approx 1.41)$ ．

题型：未知
难度：未知

收藏答案/解析

改善小区环境，争创文明家园．如图所示，某社区决定在一块长 $(AD) 16 m$ ，宽 $(AB) 9 m$ 的矩形场地 $ABCD$ 上修建三条同样宽的小路，其中两条与 $AB$ 平行，另一条与 $AD$ 平行，其余部分种草．要使草坪部分的总面积为 $112 m^{2}$ ，则小路的宽应为多少？

题型：未知
难度：未知

收藏答案/解析

今年是中华人民共和国建国70周年，襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动．学校3000名学生全部参加了竞赛，结果所有学生成绩都不低于60分（满分100分）．为了了解成绩分布情况，学校随机抽取了部分学生的成绩进行统计，得到如下不完整的统计表．根据表中所给信息，解答下列问题：

成绩 $x$ （分 $)$ 分组	频数	频率
$60 ⩽ x < 70$	15	0.30
$70 ⩽ x < 80$	$a$	0.40
$80 ⩽ x < 90$	10	$b$
$90 ⩽ x ⩽ 100$	5	0.10

（1）表中 $a =$ 　　， $b =$ 　　；

（2）这组数据的中位数落在　　范围内；

（3）判断：这组数据的众数一定落在 $70 ⩽ x < 80$ 范围内，这个说法　　（填“正确”或“错误” $)$ ；

（4）这组数据用扇形统计图表示，成绩在 $80 ⩽ x < 90$ 范围内的扇形圆心角的大小为　　；

（5）若成绩不小于80分为优秀，则全校大约有　　名学生获得优秀成绩．

题型：未知
难度：未知

收藏答案/解析