如图, 过 的圆心,交 于点 、 , 是 的切线,点 是切点,已知 , .
(1)求证: ;
(2)求 的周长.

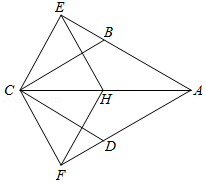
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.

如图, 是 的直径, 是 的切线, 交 于点 .
(1)若 为 的中点,证明: 是 的切线;
(2)若 , ,求 的半径 的长.

在矩形 的 边上取一点 ,将 沿 翻折,使点 恰好落在 边上点 处.
(1)如图1,若 ,求 的度数;
(2)如图2,当 ,且 时,求 的长;
(3)如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 的值.
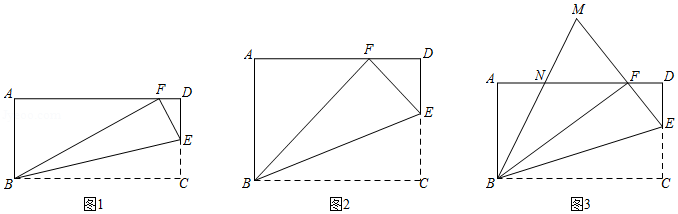
问题背景 如图(1),已知 ,求证: ;
尝试应用 如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值;
拓展创新 如图(3), 是 内一点, , , , ,直接写出 的长.

如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

如图, 中, .
(1)作点 关于 的对称点 ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图中,连接 , ,连接 ,交 于点 .
①求证:四边形 是菱形;
②取 的中点 ,连接 ,若 , ,求点 到 的距离.

已知, 为直角三角形, ,点 是射线 上一点(点 不与点 、 重合),线段 绕点 顺时针旋转 得到线段 ,连接 交射线 于点 .
(1)如图①,当 ,点 在线段 上时,线段 、 的数量关系是 ;
(2)如图②,当 ,点 在线段 的延长线时,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由.
(3)如图③,若
,点
在线段
的延长线上,
,
,求
的面积.
在中,
,
,
于点
.

(1)如图1,点,
分别在
,
上,且
,当
,
时,求线段
的长;
(2)如图2,点,
分别在
,
上,且
,求证:
;
(3)如图3,点在
的延长线上,点
在
上,且
,求证:
.
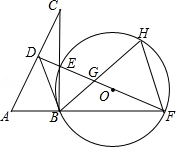
如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点 , , , 是 的外接圆, 的平分线交 于点 ,交 于点 ,连接 、 .
(1)试判断 与 的位置关系,并说明理由;
(2)当 时,求 的面积;
(3)在(2)的条件下,求 的值.
如图,在四边形 中, ,点 是 边的中点,点 恰是点 关于 所在直线的对称点.
(1)证明:四边形 为菱形;
(2)连接 交 于点 ,若 ,求线段 的长.

如图,在 中, AB AD.

(1)用尺规完成以下基本作图:在 AB上截取 AE,使得 AE= AD;作∠ BCD的平分线交 AB于点 F.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接 DE交 CF于点 P,猜想△ CDP按角分类的类型,并证明你的结论.
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.