初中数学三角形的面积解答题

如图，在平行四边形中，点是对角线的中点，点是上一点，且，连接并延长交于点．过点作的垂线，垂足为，交于点．

（1）若，，求的面积；

（2）若，求证：．

如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于、两点，与轴交于点，过点作轴于点，点是线段的中点，，，点的坐标为．

（1）求该反比例函数和一次函数的解析式；

（2）求的面积．

如图，抛物线 $y=a{x}^2+\mathit{bx}-5(a\ne 0)$ 经过点 $A(4,-5)$ ，与 $x$ 轴的负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $\mathit{OC}=5\mathit{OB}$ ，抛物线的顶点为点 $D$ ．

（1）求这条抛物线的表达式；

（2）联结 $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DA}$ ，求四边形 $\mathit{ABCD}$ 的面积；

（3）如果点 $E$ 在 $y$ 轴的正半轴上，且 $\angle \mathit{BEO}=\angle \mathit{ABC}$ ，求点 $E$ 的坐标．

（1）探索发现

如图1，在中，点在边上，与的面积分别记为与，试判断与的数量关系，并说明理由．

（2）阅读解析

小东遇到这样一个问题：如图2，在中，，，射线交于点，点、在上，且，试判断、、三条线段之间的数量关系．

小东利用一对全等三角形，经过推理使问题得以解决．

填空：①图2中的一对全等三角形为　 　；

②、、三条线段之间的数量关系为　　．

（3）类比探究

如图3，在四边形中，，与交于点，点、在射线上，且．

①判断、、三条线段之间的数量关系，并说明理由；

②若，的面积为2，直接写出四边形的面积．

图①、图②、图③均是的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点、、、、、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

（1）在图①中以线段为边画一个，使其面积为6．

（2）在图②中以线段为边画一个，使其面积为6．

（3）在图③中以线段为边画一个四边形，使其面积为9，且．

如图，在平面直角坐标系中，直线与函数的图象交于点，．过点作平行于轴交轴于点，在轴负半轴上取一点，使，且的面积是6，连接．

（1）求，，的值；

（2）求的面积．

（1）如图1，在中，，以点为中心，把逆时针旋转，得到△；再以点为中心，把顺时针旋转，得到△，连接，则与的位置关系为　　；

（2）如图2，当是锐角三角形，时，将按照（1）中的方式旋转，连接，探究与的位置关系，写出你的探究结论，并加以证明；

（3）如图3，在图2的基础上，连接，若，△的面积为4，则△的面积为　　．

数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所得两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．

（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》

请根据该图完成这个推论的证明过程．

证明：，　　　　．

易知，，　　　　，　　　　．

可得．

如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

△ABC在平面直角坐标系xOy中的位置如图所示．

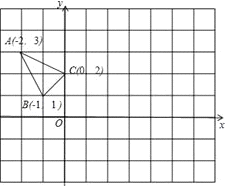
（1）作△ABC关于y轴成轴对称的△A₁B₁C₁；
（2）将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂；则此三角形的面积为       ．
（3）在x轴上求作一点P，使PA₁+PC₂的值最小，点P的坐标为       ．

已知关于x的方程x²－（m＋2）x＋（2m－1）=0的一个根是2，请求出方程的另一个根，并求以此两根为边长的直角三角形的面积。