(回顾)
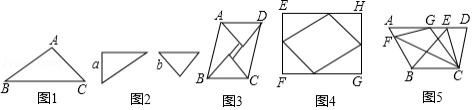
如图1, 中, , , ,则 的面积等于 .
(探究)
图2是同学们熟悉的一副三角尺,一个含有 的角,较短的直角边长为 ;另一个含有 的角,直角边长为 ,小明用两副这样的三角尺拼成一个平行四边形 (如图 ,用了两种不同的方法计算它的面积,从而推出 ,小丽用两副这样的三角尺拼成了一个矩形 (如图 ,也推出 ,请你写出小明或小丽推出 的具体说理过程.
(应用)
在四边形 中, , , , , (如图5)
(1)点 在 上,设 ,求 的最小值;
(2)点 在 上,将 沿 翻折,点 落在 上的点 处,点 是 的中点吗?说明理由.
操作:“如图1, 是平面直角坐标系中一点 轴上的点除外),过点 作 轴于点 ,点 绕点 逆时针旋转 得到点 .”我们将此由点 得到点 的操作称为点的 变换.
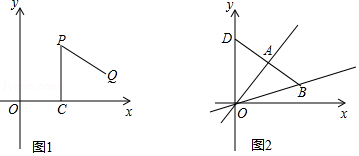
(1)点 经过 变换后得到的点 的坐标为 ;若点 经过 变换后得到点 ,则点 的坐标为 .
(2) 是函数 图象上异于原点 的任意一点,经过 变换后得到点 .
①求经过点 ,点 的直线的函数表达式;
②如图2,直线 交 轴于点 ,求 的面积与 的面积之比.
如图,在平面直角坐标系中,已知点 ,以原点 为圆心、3为半径作圆. 从点 出发,以每秒1个单位的速度沿 轴正半轴运动,运动时间为 .连接 ,将 沿 翻折,得到 .求 有一边所在直线与 相切时 的值.
