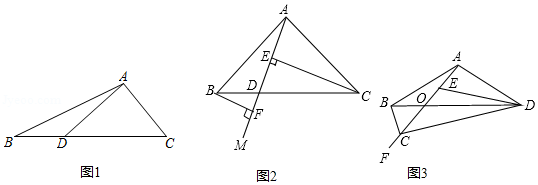
(1)探索发现
如图1,在中,点在边上,与的面积分别记为与,试判断与的数量关系,并说明理由.
(2)阅读解析
小东遇到这样一个问题:如图2,在中,,,射线交于点,点、在上,且,试判断、、三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为 ;
②、、三条线段之间的数量关系为 .
(3)类比探究
如图3,在四边形中,,与交于点,点、在射线上,且.
①判断、、三条线段之间的数量关系,并说明理由;
②若,的面积为2,直接写出四边形的面积.
相关知识点
推荐套卷

 -2.5=
-2.5= .
.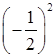 ×(-2)3+
×(-2)3+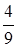 ×(-3)3.
×(-3)3. ABCD的两条对角线线交于O,且
ABCD的两条对角线线交于O,且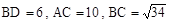 。
。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号