如图,点,
,
是直线
与反比例函数
图象的两个交点,
轴,垂足为点
,已知
,连接
,
,
.
(1)求直线的表达式;
(2)和
的面积分别为
,
.求
.

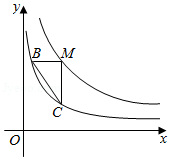
如图,点 在函数 的图象上,过点 分别作 轴和 轴的平行线交函数 的图象于点 、 .
(1)若点 的坐标为 .
①求 、 两点的坐标;
②求直线 的解析式;
(2)求 的面积.
双曲线为常数,且
与直线
,交于
,
,
两点.
(1)求与
的值;
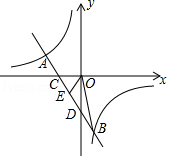
(2)如图,直线交
轴于点
,交
轴于点
,若点
为
的中点,求
的面积.
如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

如图,在平面直角坐标系中,一次函数
和
的图象相交于点
,反比例函数
的图象经过点
.
(1)求反比例函数的表达式;
(2)设一次函数的图象与反比例函数
的图象的另一个交点为
,连接
,求
的面积.

阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.

如图,在平行四边形中,点
在边
上,连接
,
,垂足为
,交
于点
,
,垂足为
,
,垂足为
,交
于点
,点
是
上一点,连接
.
(1)若,
,
,求
的面积.
(2)若,
,求证:
.

如图,平面直角坐标系中,已知点 的坐标为 .
(1)请用直尺(不带刻度)和圆规作一条直线 ,它与 轴和 轴的正半轴分别交于点 和点 ,且使 , 与 的面积相等.(作图不必写作法,但要保留作图痕迹.
(2)问:(1)中这样的直线 是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线 ,并写出与之对应的函数表达式.
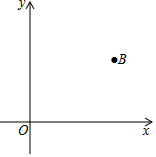
如图,在平面直角坐标系中,一次函数的图象与反比例函数
的图象交于
、
两点,与
轴交于点
,过点
作
轴于点
,点
是线段
的中点,
,
,点
的坐标为
.
(1)求该反比例函数和一次函数的解析式;
(2)求的面积.

如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.

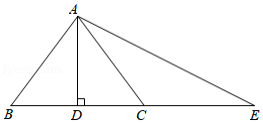
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
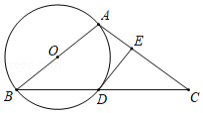
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个一边长为 ,面积为6的等腰三角形.

如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
(1)画出与 关于 轴对称的△ ;
(2)将 绕点 顺时针旋转 得到△ , 弧是点 所经过的路径,则旋转中心 的坐标为 ;
(3)求图中阴影部分的面积(结果保留 .

(1)探索发现
如图1,在中,点
在边
上,
与
的面积分别记为
与
,试判断
与
的数量关系,并说明理由.
(2)阅读解析
小东遇到这样一个问题:如图2,在中,
,
,射线
交
于点
,点
、
在
上,且
,试判断
、
、
三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为 ;
②、
、
三条线段之间的数量关系为 .
(3)类比探究
如图3,在四边形中,
,
与
交于点
,点
、
在射线
上,且
.
①判断、
、
三条线段之间的数量关系,并说明理由;
②若,
的面积为2,直接写出四边形
的面积.
