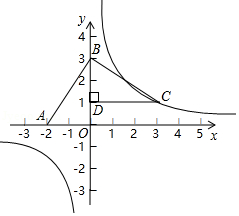
如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.
相关知识点
推荐套卷
如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.
