甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过2000元的电器,超出的金额按80℅收取;乙商场规定:凡超过1500元的电器,超出的金额按90℅收取.某顾客购买的电器价格是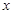 元.
元.
(1)当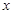 =1600时,该顾客应选择在 商场购买比较合算;
=1600时,该顾客应选择在 商场购买比较合算;
(2)当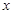 >2000时,分别用代数式表示在两家商场购买电器所需付的费用;
>2000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当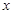 =3000时,该顾客应选择哪一家商场购买比较合算?说明理由.
=3000时,该顾客应选择哪一家商场购买比较合算?说明理由.
甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过2000元的电器,超出的金额按80℅收取;乙商场规定:凡超过1500元的电器,超出的金额按90℅收取.某顾客购买的电器价格是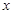 元.
元.
(1)当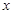 =1600时,该顾客应选择在 商场购买比较合算;
=1600时,该顾客应选择在 商场购买比较合算;
(2)当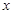 >2000时,分别用代数式表示在两家商场购买电器所需付的费用;
>2000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当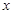 =3000时,该顾客应选择哪一家商场购买比较合算?说明理由.
=3000时,该顾客应选择哪一家商场购买比较合算?说明理由.